大模型后训练的动力学 阅读笔记

本文是 ICLR 2025 Outstanding Paper 《Learning Dynamics of LLM Finetuning》的阅读笔记和评介，以一种简略的方式介绍一部分该文精华内容。有趣的是，这样一个关心模型训练本质的研究，为之前观察到的很多表面现象给出了更深刻的解释，包括重复、幻觉、离线策略DPO训练中所有响应的信心衰减等，未尝不是一种无心插柳柳成荫。

1. 问题定义

如标题所言，该文专注于大模型后训练中的动力学问题。尽管“动力学”很精准地表达了该文的中心，但对于未接触过系统研究的读者则可以表述得更直白：模型后训练无非就是用额外的数据进一步调节模型，那这些数据的使用究竟给模型带来了什么变化？该问题无疑会让人产生更多联想：后训练过程中发生了什么，有什么影响，如何观测这些结果，如何预期在真实使用场景中它会有什么表现？这些问题背后暗示着对理解大模型背后机制的解释性理论的憧憬，且该解释最好是精确的，而非半桶水似的泛泛而谈、充满了修辞手法却停在抽象层面。

这么复杂的问题该如何解答呢？作者首先将“模型训练动力学”问题具体表达为：模型参数 \(\theta\) 的 变化如何影响模型输出 \(f_\theta\)的变化，即 \(\Delta\theta\) 和 \(\Delta f_\theta\) 的关系。假如用最普通的随机梯度下降方法，则该问题可以进一步转化为样本之间的联系：

其中 \(x_u\) 是训练样本，\(x_o\) 是推理样本。

2. 形式拆解

到这里 \(\Delta\theta\) 和 \(\Delta f_\theta\) 虽然定义清楚了，但二者还没直接联系起来，还需要继续推导形式上的关系。

作者引入了常规的记号继续推导：给定输入 \(x\) ，输出是一组预测 \(y=\{y_1, \dots,y_L\}\in \mathcal{V}^L\)，其中 \(\mathcal{V}\) 是词表大小，即目标域。模型首先计算 \(x\) 的 logits 即\(z=h_\theta(x) \in \mathbb{R}^{V\times L}\)，再做 Softmax 运算求出 \(y=\{y_i\}^L\) 的概率，即\(\pi=\text{softmax}(z)\)。 可以通过衡量其对数似然 \(\log\pi_\theta(y\mid x)\) 来观测模型对输出的信心。上式变为：

如果只考虑 \(L=1\)，即只输出一个标签，问题就可以看成普通的分类。此时就可以继续将 \(\Delta f(\mathbf{x}_o)\) 分解成有物理意义的三个因子，用于解释 \(\Delta\theta\) 和\(\Delta f_\theta(\cdot)\) 的关系。即如下命题：

Proposition 1. Let \(\pi = \text{Softmax}(\mathbf{z})\) and \(\mathbf{z} = h_{\theta}(\mathbf{x})\). The one-step learning dynamics decompose as

where \(\mathcal{A}^t(\mathbf{x}_o)=\nabla_{\mathbf{z}} \log \pi_{\theta^t}(\mathbf{x}_o) = I - \mathbf{1} \pi_{\theta^t}^{\top}(\mathbf{x}_o)\), \(\mathcal{K}^t(\mathbf{x}_o, \mathbf{x}_u) = (\nabla_{\theta} \mathbf{z}(\mathbf{x}_o)|_{\theta^t})(\nabla_{\theta} \mathbf{z}(\mathbf{x}_u)|_{\theta^t})^{\top}\) is the empirical neural tangent kernel of the logit network \(\mathbf{z}\), and \(\mathcal{G}^t(\mathbf{x}_u, \mathbf{y}_u) = \nabla_{\mathbf{z}} \mathcal{L}(\mathbf{x}_u, \mathbf{y}_u)|_{\mathbf{z}^t}\).

这三个因子具有重要意义，其中后两个贯穿本文的分析过程：

• A只跟模型当前预测有关（t时刻），跟本文所关心的变化量无关
• K是一个经验的“神经正切核”，代表了两个样本在特定模型眼里的相似性（没有解释性）
• G和损失函数有关，为模型训练提供“能源”（借鉴动力学的比喻）

基于MNIST的解释

以经典的分类任务 MNIST 作为案例研究可以粗略对应上面两个因子的解释：

从单步动态可发现：

• 训练样本的预测概率被G项dominate
• 相似样本的概率也被拉大（即使预测错误）

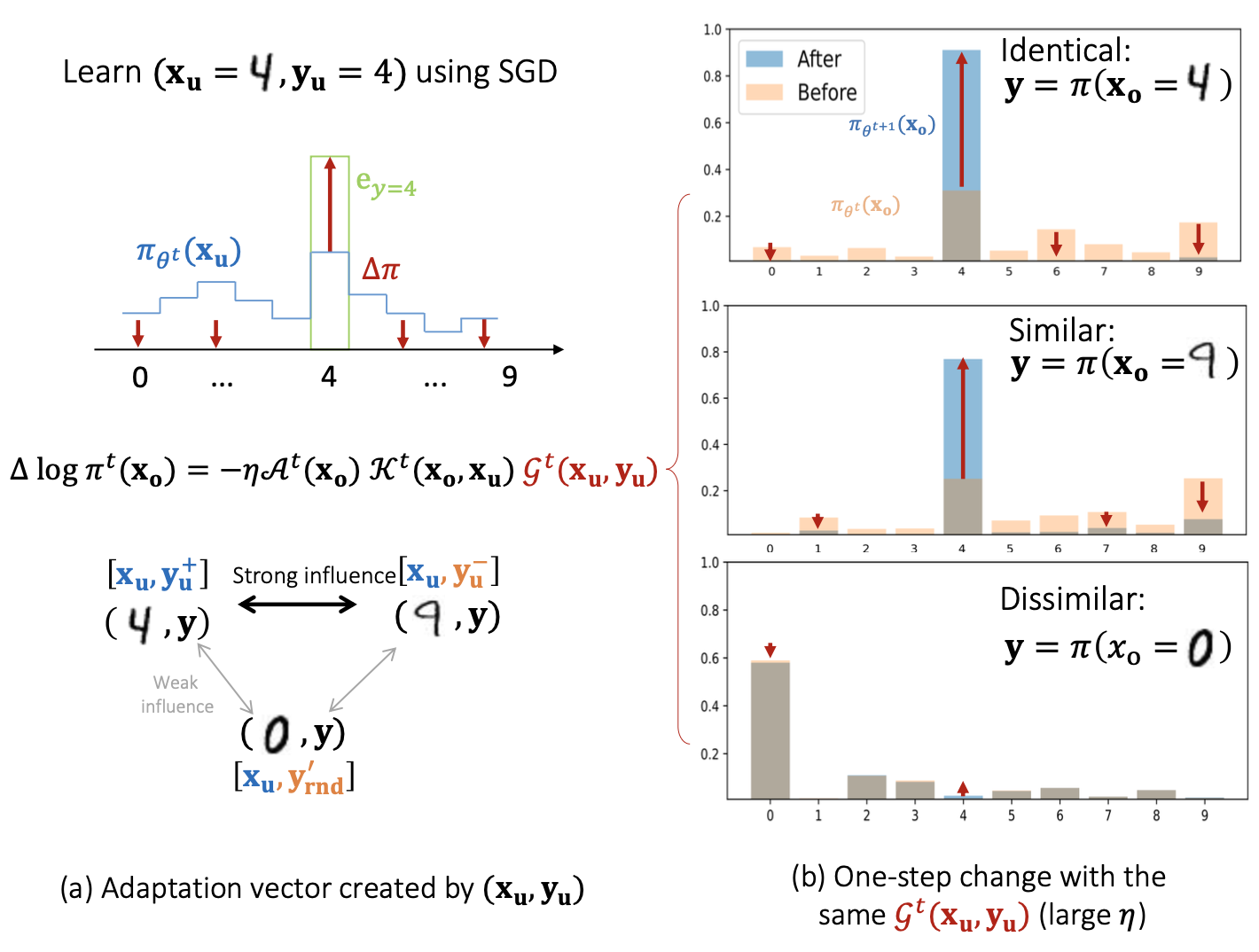
累计的观测也验证了该结论：

• 训练结束时4和9相互有更高信心，而不相似的0没有太大
• 把每个类别分别平均，可以观察到除了对角线之外的其他高亮

3. 大模型的分解

对于大模型，最大的区别在于输出的 y 是不定长的句子。但采取的方式非常简单，直接将前面的 y 扩张出一个长度维度叠起来，并拼接大模型的输入 x 和输出 y。

SFT

其损失为：

相应的各项分解于 MNIST 的例子很接近：

其中 \(\mathcal{G}_{\text{SFT}}^t(\boldsymbol{\chi}_u) = \pi_{\theta^t}(\mathbf{y} \mid \boldsymbol{\chi}_u) - \mathbf{y}_u\)。证明从略。这里唯一的区别是：在 MNIST 中 x 是样本，现在的 \(\chi\) 是 x 和 y，于是可以评估同一个 prompt 的两个输出的相互影响。

因此对SFT的预测和前面类似：正样本和它的相似样本都会被施加一个概率增大的力。

DPO

其损失为：

各项分解为：

其中 a 是 sigmoid 的值，可理解为当前策略对正负样本的区分能力，当a比较小时，正负样本带来的能量就比较小。

beta 是个超参，控制参考模型的充当正则项的作用大小，当策略很差时，增大 beta 能加速靠近参考模型，而当策略较好，更大beta也会增大 a 从而弱化能量源的作用。这个分析直接从上式给出，与DPO原文关于参考模型的正则化作用相吻合。

此处没有讨论正负样本来源，因此它既可以是离线的，也可以是在线的。由于离线的正负样本可能是模型都不偏好的，此时会产生非预期的行为，而在线的算法改进可以缓解该问题。

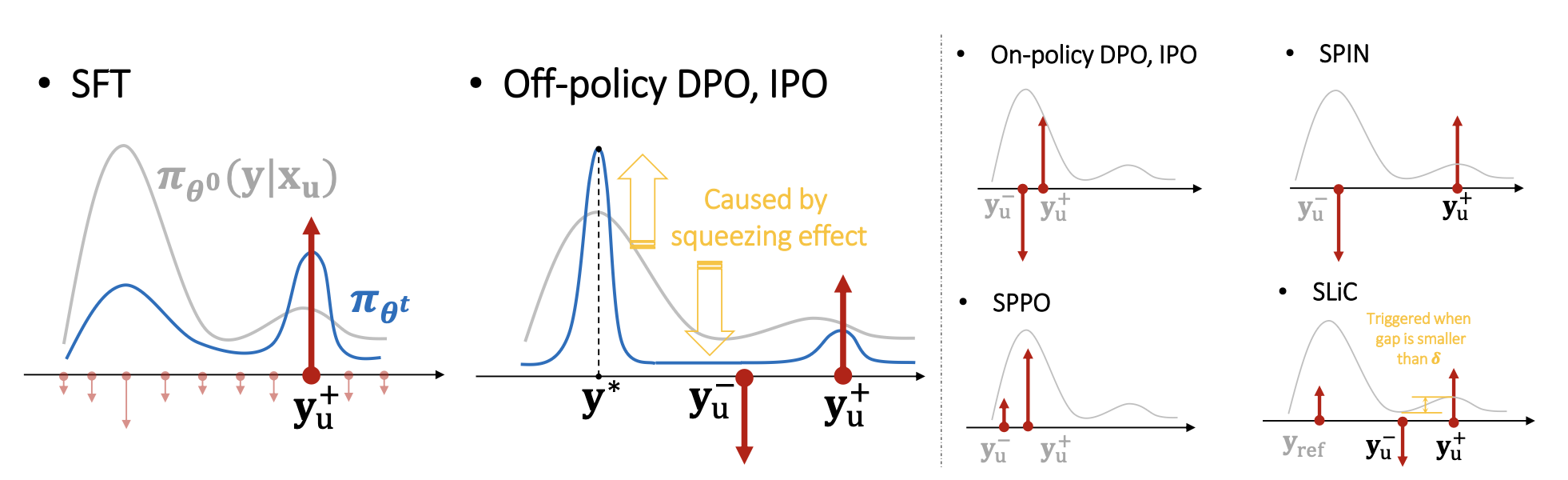
挤压效应

SFT 和 DPO 的关键区别在负样本的使用。正负样本在强化后概率都可能降低，那概率去哪了？作者预测了一个概率挤压问题（L=1情形）：

• 负样本训练导致负样本概率降低
• 概率被主要分配到排除负样本之外最高的样本 y*
• 强者越强，弱者越弱
• 大模型往往只预测少量几个高概率输出，因而所有非峰值的 token 概率全部降低
• 负样本的概率越低，训练后唯一的极值 token 概率增加最多

但是，该问题由于有正负样本同时作用、自回归、NTK等多重影响，分析并没有那么容易。作者仅在逻辑回归模型上分析地证明了该现象，后续会通过实验验证。但另一方面，假如该现象确实存在，那么可以预测坏处。作者展示了 SFT 阶段越长、DPO带来的挤压作用越严重。

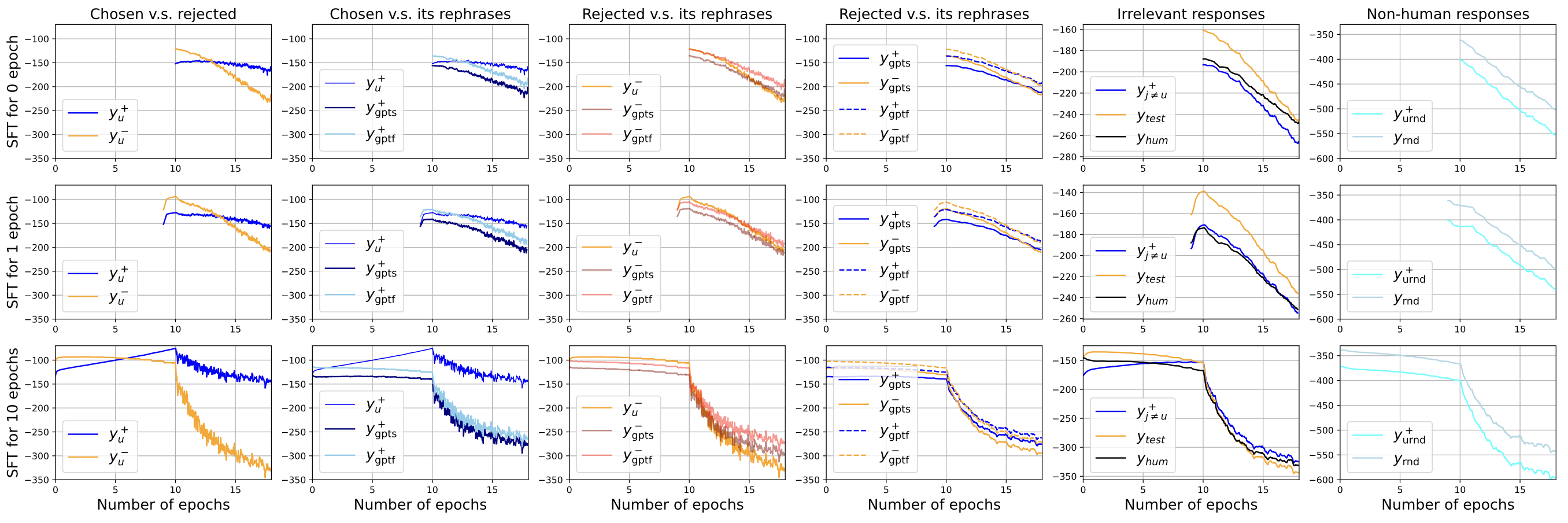
因此，由于挤压作用的负面影响，模型的概率最大输出会更大，极易在偏好训练后产生重复效应。

4. 实验证据

探测手段

模型：pythia-410M/1B/1.4B/2.8B 和 Qwen1.5-0.5B/1.8B 数据集：Anthropic-HH 和 UltraFeedback

构造探测集合，从训练集中选出500个样本：x、y+、y-，按照不同策略构造更多正负样本，分别实验。

SFT

验证方法：每25步验证一次全集，bs=4时为每100个样本（全集约5k）

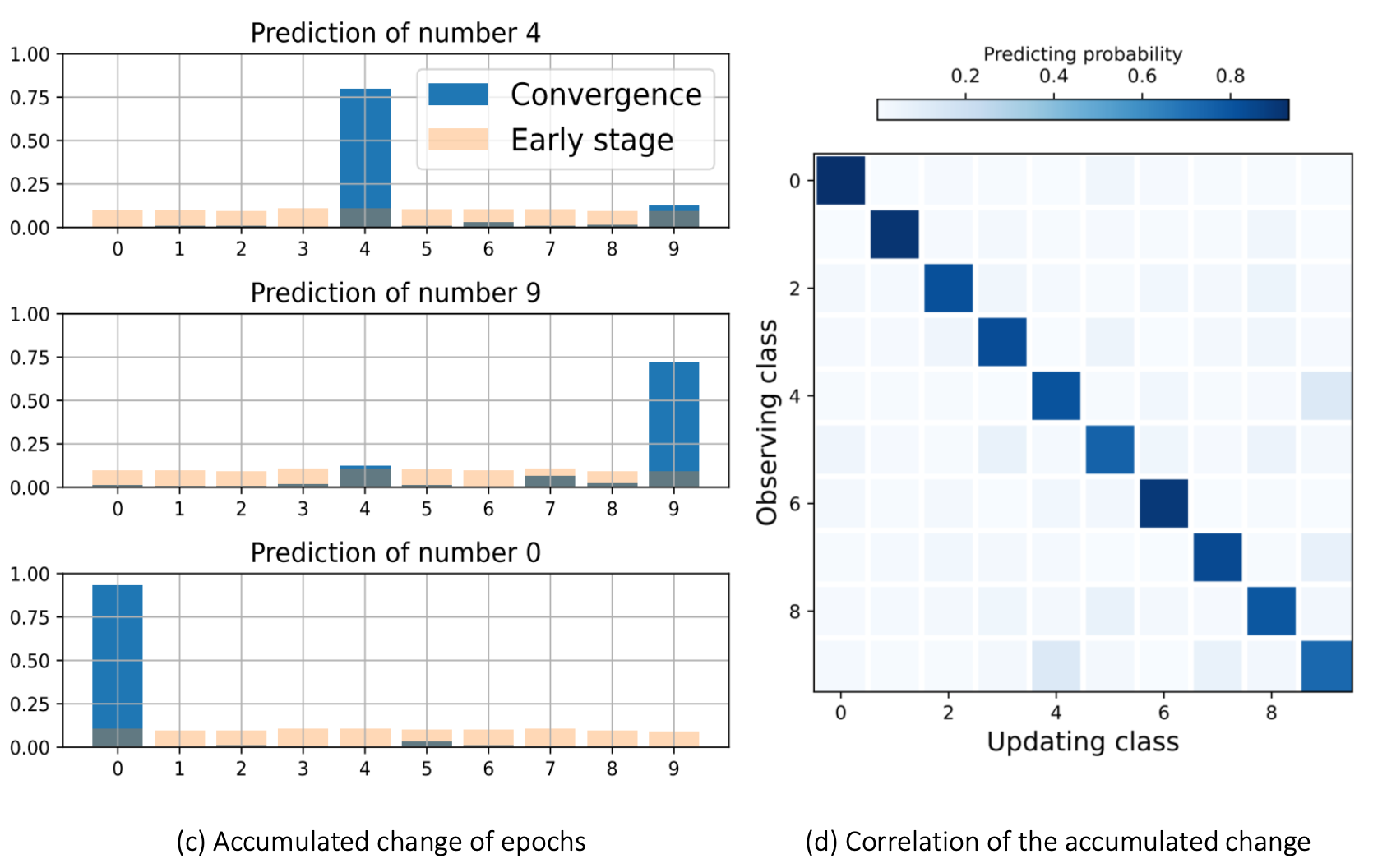
符合预期结论：

• 一开始猛增，由于NTK相似性+梯度能量共同作用，尽管这些样本没见过
• 随着模型增强，梯度作用降低，非正样本的概率逐步下降
• 随机答案由于相似性很低，一直在大幅下降

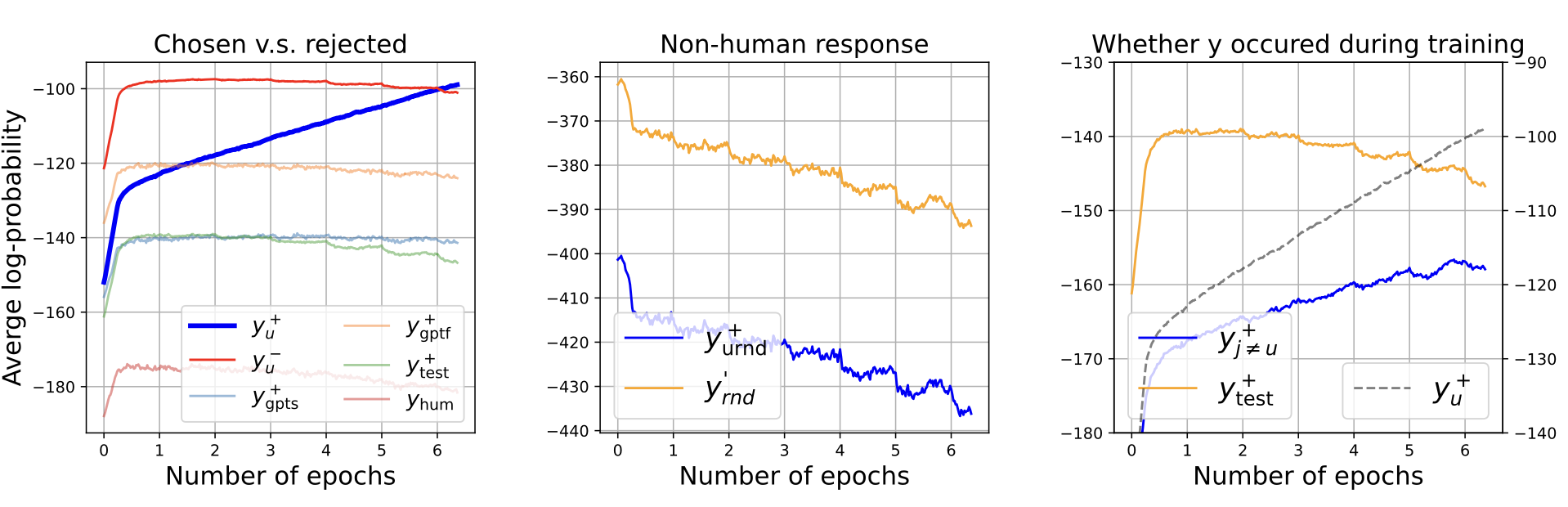
此外，随着训练持续，嫁接其他训练样本的输出也有增加趋势（当然，增加趋势远不如样本自己）。这解释了SFT幻觉的产生实质：模型逐渐挪用其他训练样本的答案来回答这个答案。

通过概率来估计相似度，横轴是更新样本，纵轴是观测样本。即给定 GPT 生成的样本进行训练，无论哪种GPT样本居然都有较高的概率，说明模型生成的数据可能存在暂时不能言明的指纹。（实际设置存疑）

DPO

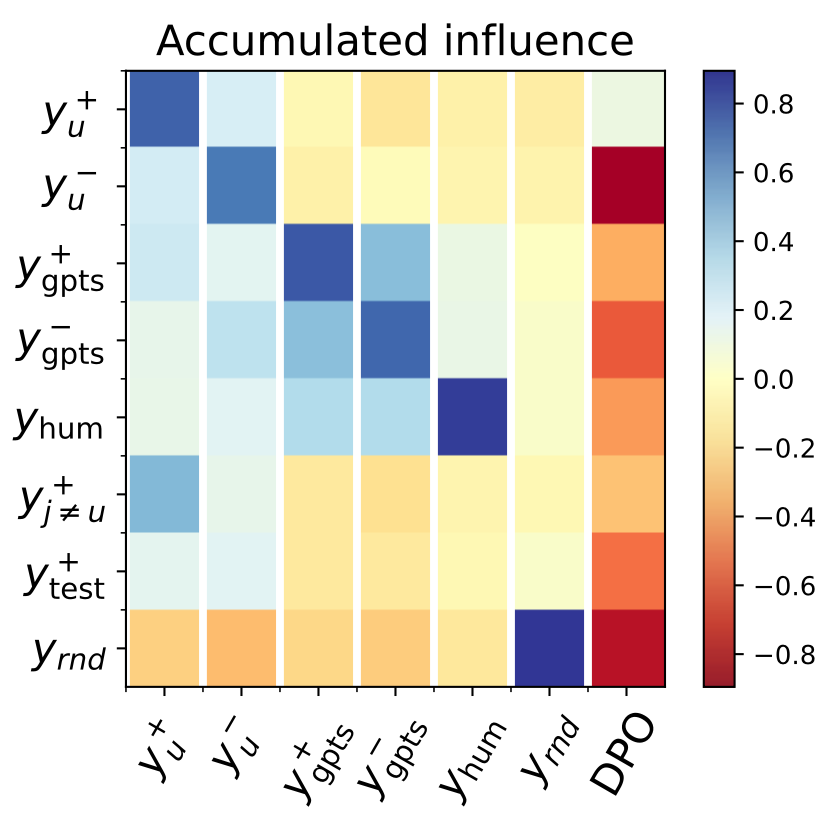
离线的DPO实验也符合预期：

• 正负样本概率都会逐渐下降（验证了NTK较大，but其实应该相反，检验NTK大小的区别）
• 但正例（及其复述）降得缓慢一些，因为正例有一个向上推力
• 模型概率最大的回复会强者恒强

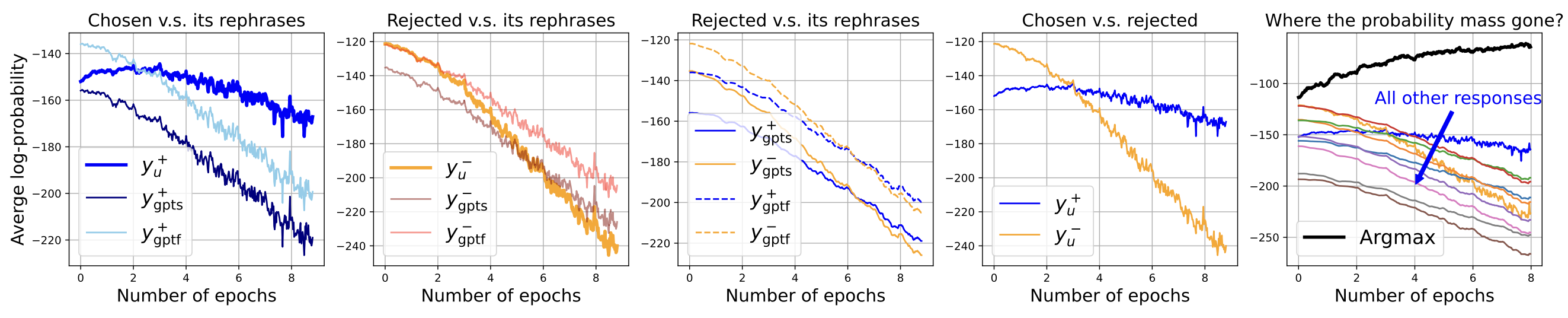
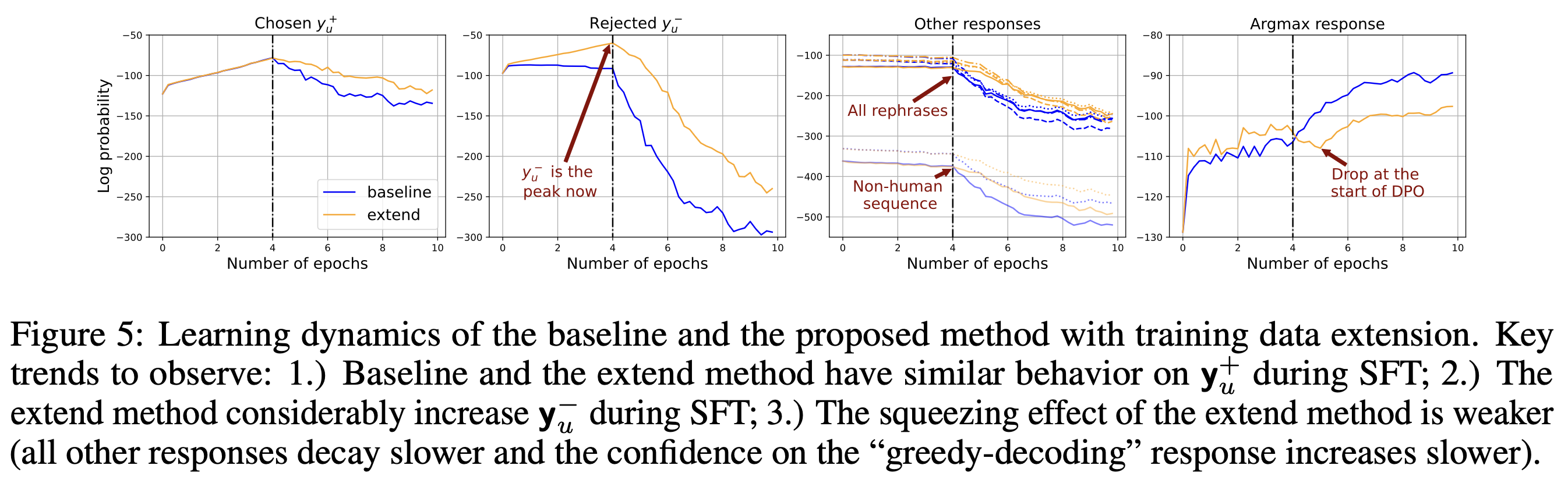
对于DPO，作者提出，首先将正负样本都做一遍 SFT，让负例也有一定的概率，然后再做DPO。实验确认：

• 可以减缓正例的概率降低的速度
• DPO概率最大的策略有少许下降，后续概率上升也不再极端

5. 结论

理论贡献：从动态的视角给了一种解释性框架（模型的“示波器”），统一地解释了模型后训练的很多算法（包括正文中没有展开的一众DPO扩展）

现象解释：从更根本的角度，一股脑地解释了偏好训练后的重复现象、SFT后的幻觉、DPO后输出的退化等多种现象。

应用价值：从动力学角度对样本的删减、多样性的评估、样本之间的相互作用等任务给出了可验证的路线。

附

命题1证明

可以将上述命题贴入不同AI看它们怎么证明的。

Proposition 1. Let \(\pi = \text{Softmax}(\mathbf{z})\) and \(\mathbf{z} = h_{\theta}(\mathbf{x})\). The one-step learning dynamics decompose as

\( \Delta \log \pi^t(\mathbf{y} \mid \mathbf{x}o) = \underbrace{-\eta}{V \times 1} \underbrace{\mathcal{A}^t(\mathbf{x}o)}{V \times V} \underbrace{\mathcal{K}^t(\mathbf{x}o, \mathbf{x}_u)}{V \times V} \underbrace{\mathcal{G}^t(\mathbf{x}u, \mathbf{y}_u)}{V \times 1} + \mathcal{O}(\eta^2 |\nabla_{\theta} \mathbf{z}(\mathbf{x}u)|{\text{op}}^2), \)

where \(\mathcal{A}^t(\mathbf{x}o) = \nabla{\mathbf{z}} \log \pi_{\theta^t}(\mathbf{x}o) = I - \mathbf{1} \pi{\theta^t}^{\top}(\mathbf{x}o)\), \(\mathcal{K}^t(\mathbf{x}_o, \mathbf{x}_u) = (\nabla{\theta} \mathbf{z}(\mathbf{x}o)|{\theta^t})(\nabla_{\theta} \mathbf{z}(\mathbf{x}u)|{\theta^t})^{\top}\) is the empirical neural tangent kernel of the logit network \(z\), and \(\mathcal{G}^t(\mathbf{x}u, \mathbf{y}_u) = \nabla{\mathbf{z}} \mathcal{L}(\mathbf{x}u, \mathbf{y}_u)|{\mathbf{z}^t}\).

ChatGPT o4-mini

下面给出一个基于一阶泰勒展开和链式法则的证明思路。

记号约定

• 令 \(z^t(x)=h_{\theta^t}(x)\)，\ \(\pi^t(x)=\text{Softmax}\bigl(z^t(x)\bigr)\)。
• 在时刻 \(t\) 做一次梯度下降更新：

1. 参数更新诱导的 logit 变化

对 \(z(x)=h_\theta(x)\) 作一阶泰勒展开，

代入 \(\theta^{t+1}-\theta^t=-\eta\,\nabla_\theta\mathcal{L}_u\big|_{\theta^t}\) （其中简写 \(\mathcal{L}_u=\mathcal{L}(x_u,y_u)\) ）得

注意到

定义

于是对任意 \(x\) 都有

2. 从 logit 变化到 log‑policy 变化

我们关心目标状态 \(x_o\) 下的 \(\log\pi^t(y\!\mid x_o)\)。令

则

对 \(f\) 也做一阶泰勒展开：

注意

（这是 softmax log‑梯度的标准形式）。于是

\(\Delta\log\pi^t(y\mid x_o) =\log\pi^{t+1}(y\mid x_o) -\log\pi^t(y\mid x_o)\)\(\quad\approx A^t(x_o)^\top \Bigl[\,-\eta\,\mathcal{K}^t(x_o,x_u)\,G^t_u\Bigr] \;+\;O\bigl(\eta^2\,\|\nabla_\theta h_\theta(x_u)\|_{\mathrm{op}}^2\bigr).\)

去掉“\(\top\)”的位置符号并整理标量积，就得到了命题中式（3）：

小结：

1. 用参数梯度下降的一阶泰勒展开，把 \(\theta\) 更新诱导到 logit \(z\) 上；
2. 再对 log‑softmax 作一阶泰勒展开，得到 log‑policy 的变化；
3. 识别出雅可比积 \(\nabla_\theta h\;\nabla_\theta h^\top\) 是 NTK，\(\nabla_z\log\pi\) 给出 \(A^t\)，最后组合即可。