奖励模型之解放思想
沿着RLHF的角度进行奖励模型近期相关发展的综述笔记。
1. RL 算法 vs Generalized Reward Design
解耦视角:
- RL算法自己可以改进,但不妨碍任务运用的讨论。
- 但RL算法离实现更近,更容易受客观约束,同时也是复杂度来源

其他相似定位的算法:
- ReMAX
- RLOO
讨论范围限制:
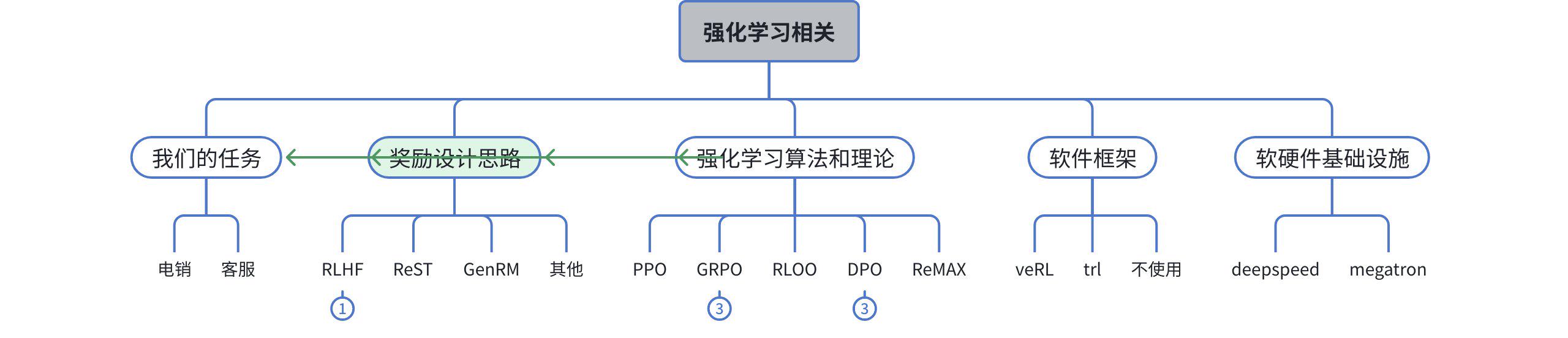
2. 奖励模型发展类别
RLHF最早由InstructGPT引入,逐步发展成了一个训练流程中必备步骤。主要流程:
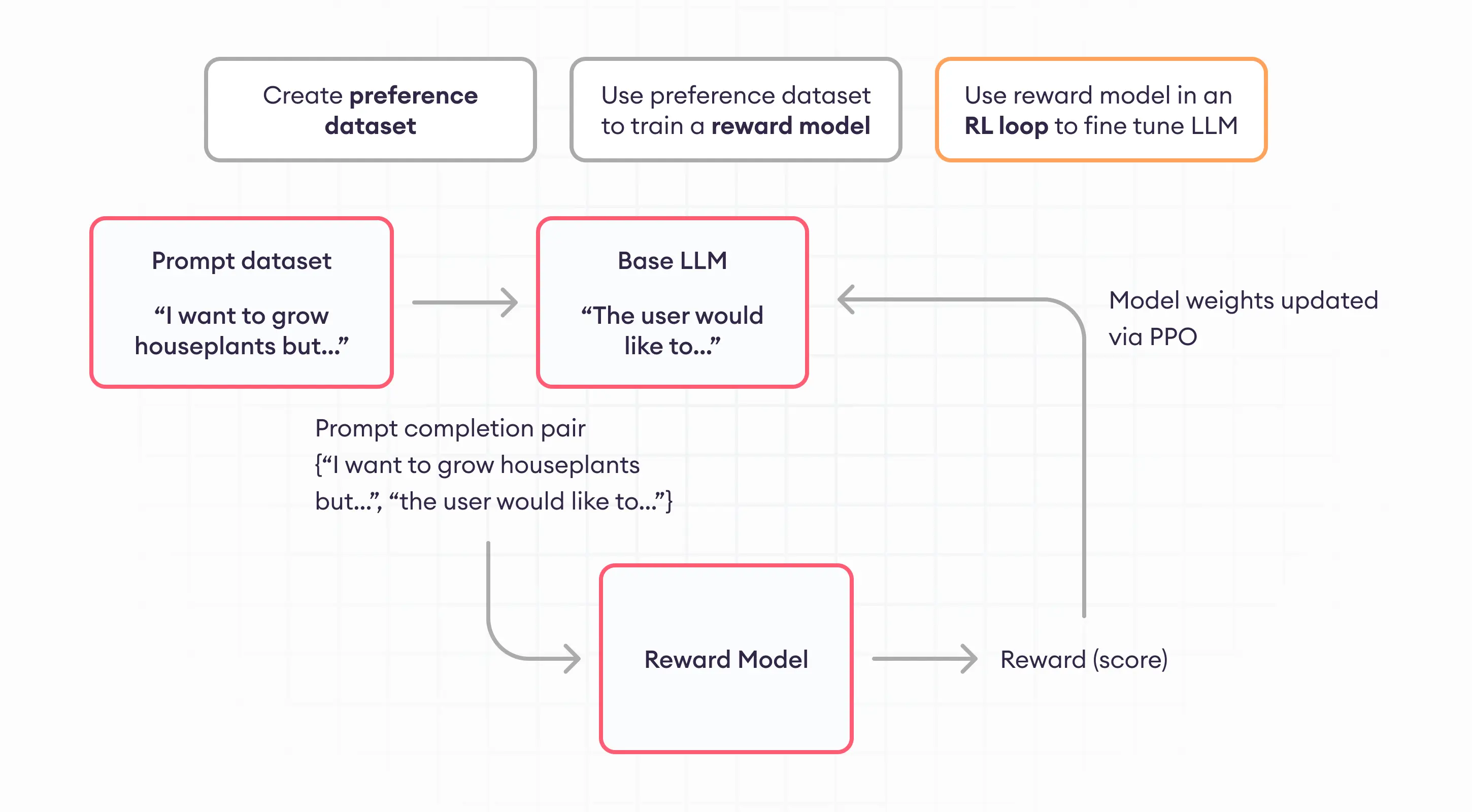
各类后续改进或发展可由上图各模块定位。
reward整理:
- https://blog.csdn.net/qq_35812205/article/details/133563158
- https://blog.csdn.net/qq_51399582/article/details/146413325
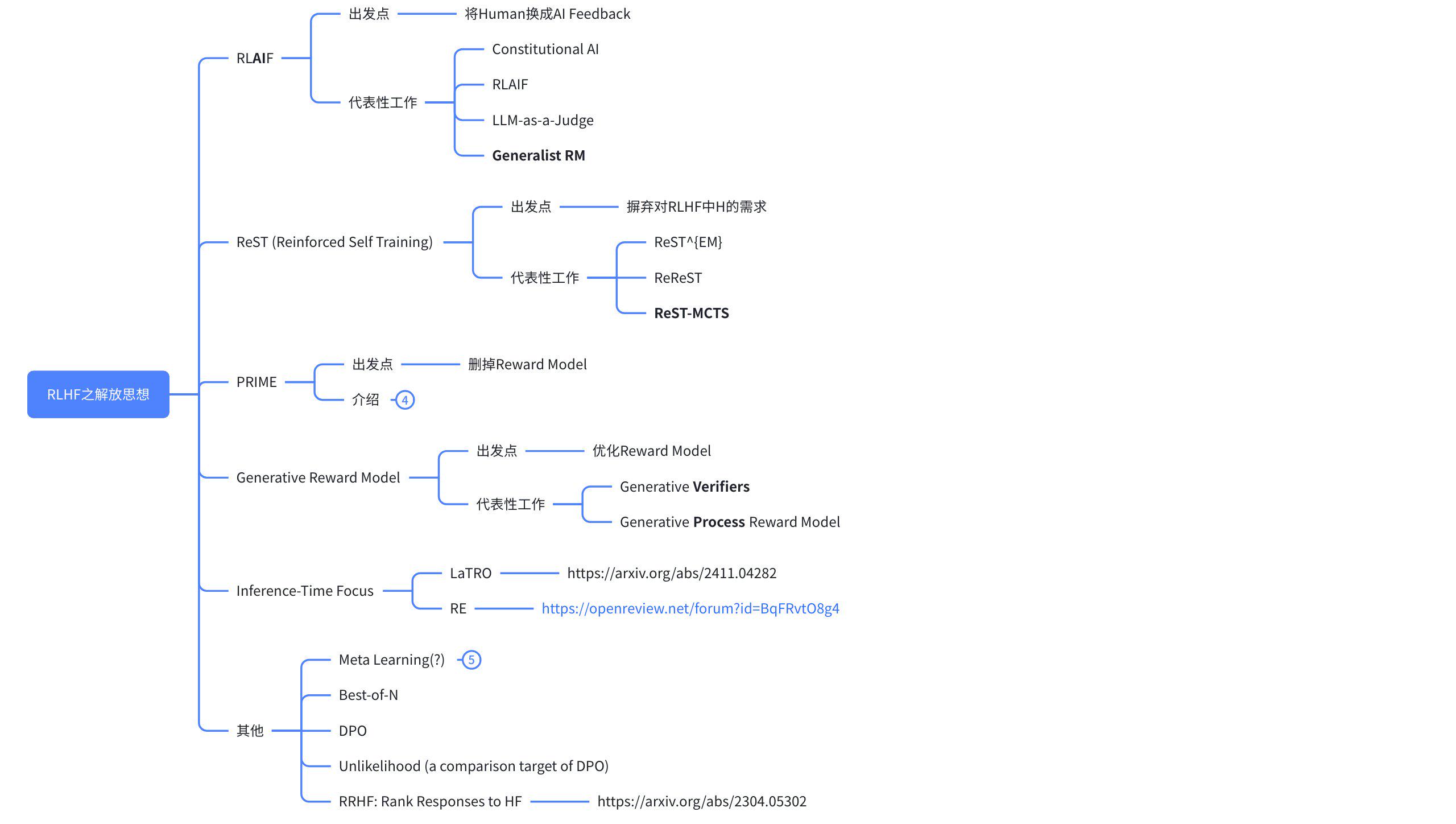
3. RLAIF
将AI模型换掉人:
- 直接作为Reward Model训练 https://arxiv.org/pdf/2309.00267
- 或者训练一个大模型的AI再强化原策略模型 https://arxiv.org/abs/2402.12366
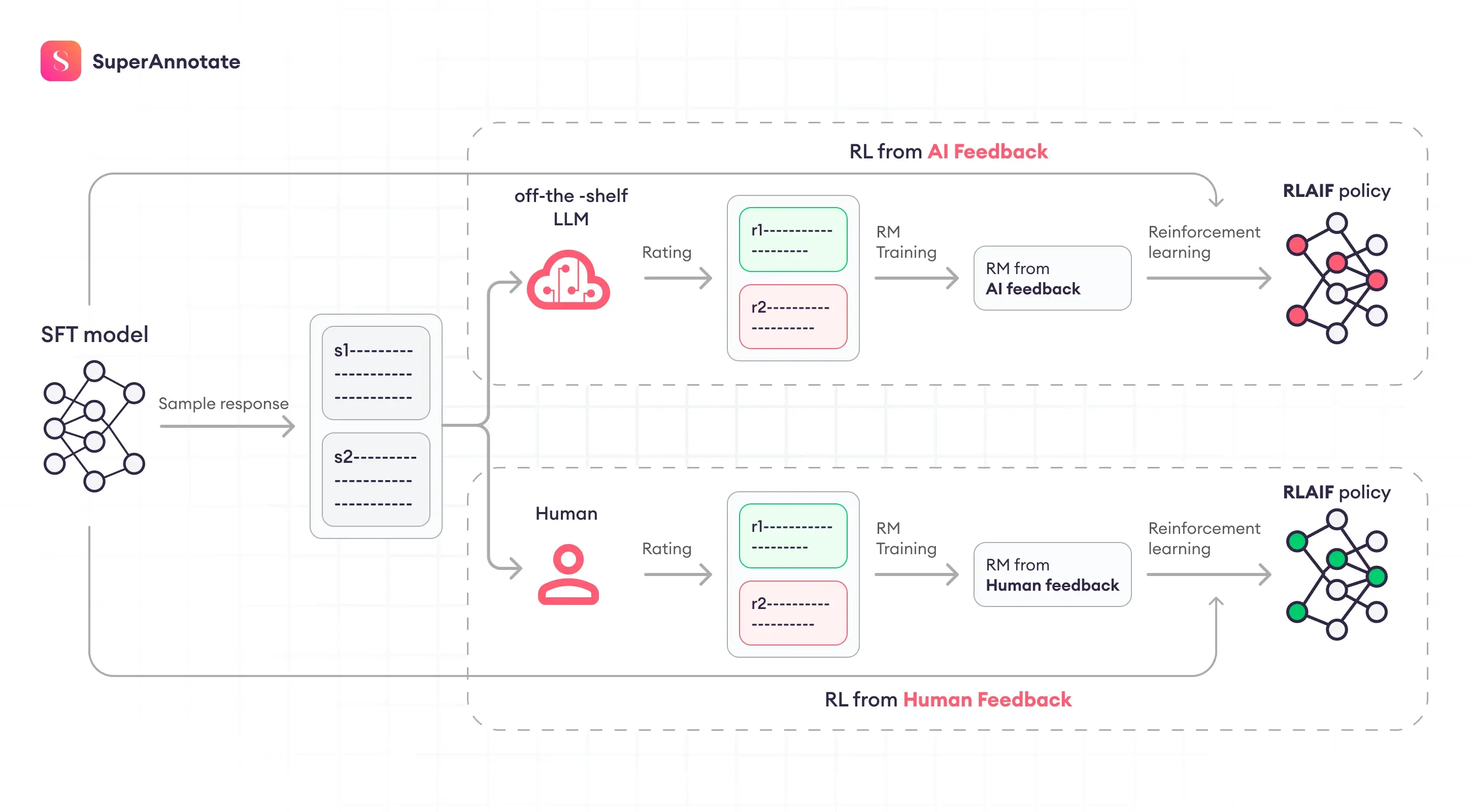
已证实其工作原理本身就是蒸馏大模型,而非强化过程:
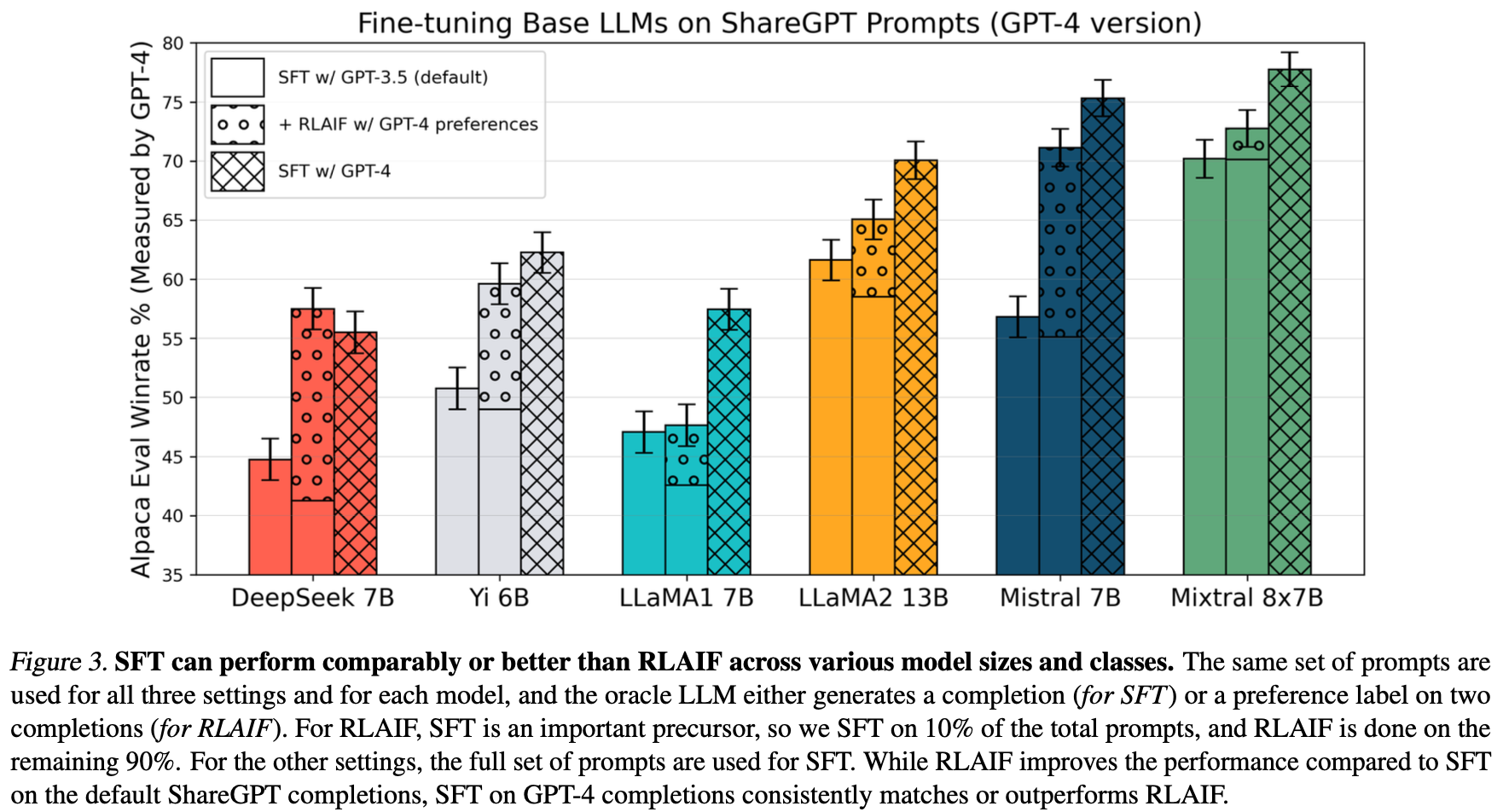
Image Credit: A Critical Evaluation of AI Feedback for Aligning Large Language Models
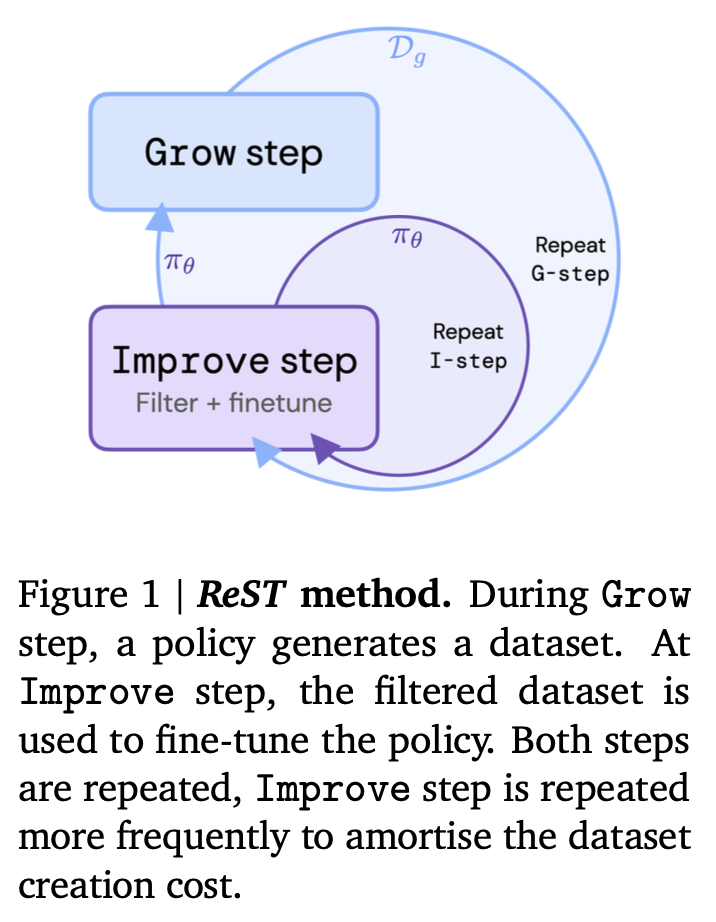
4. ReST
Reinforced Self-Training,主要由DeepMind提出和发展,最新有清华的持续改进。关键改动在于:从人类给出偏好得分,改为被训练的模型自己打出偏好得分。
标准版ReST

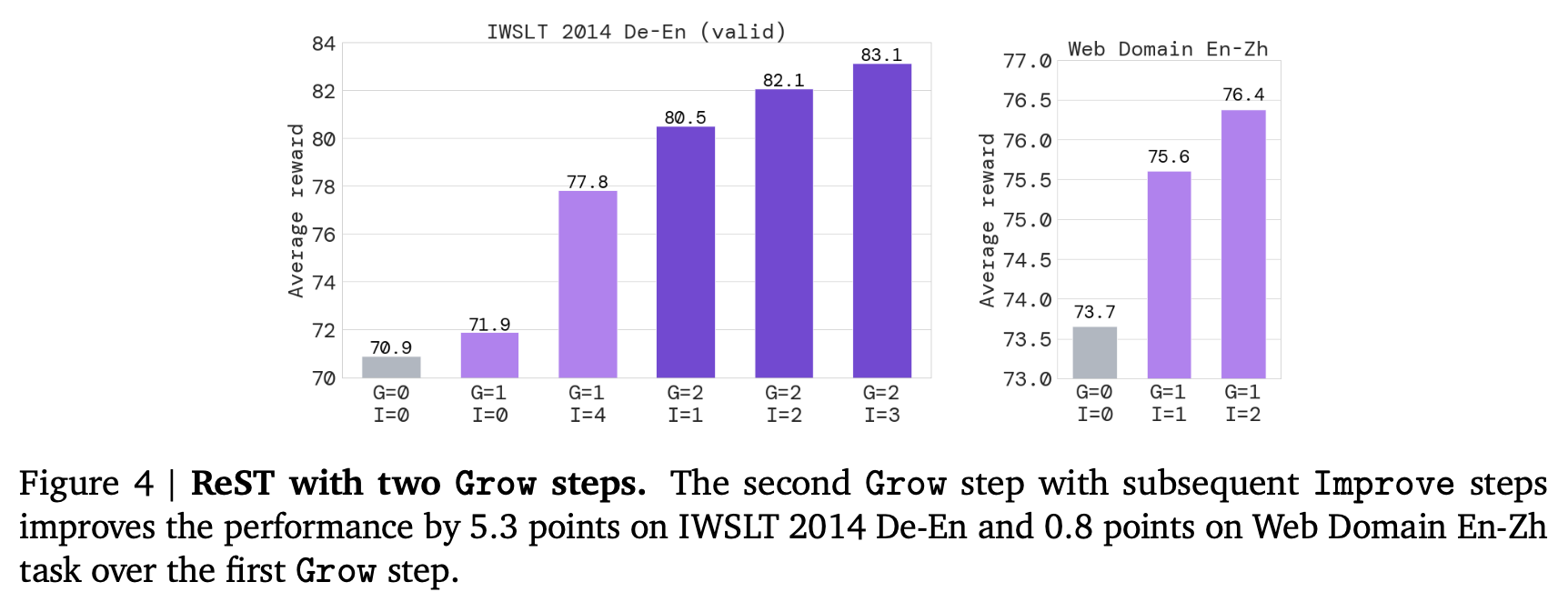
仅验证机器翻译的性能:
为什么它会有效?
\[\nabla J(\theta) = -\mathbb{E}_{ x \sim \mathcal{D} } \left[ \lambda \mathbb{E}_{y \sim \pi_{\theta'}(y|x)} \left[ F(x, y; \tau) \nabla \log \pi_{\theta}(y \mid x) \right] + (1 - \lambda) \mathbb{E}_{ y \sim p(y|x)} \left[ F(x, y; \tau) \nabla \log \pi_{\theta}(y \mid x) \right] \right]\]- 左侧一开始是个Online的策略梯度,过滤函数F可以看作是个Q(x, y)的值函数
- 右侧也根据过滤器F进行了挑选,但可看作是保证了真实数据不偏的mode collapse手段
猜测:这实际上构建了一个动态的选择最适合自己的样本的过程,只要数据集构建合理,该方式可以自动去噪并获取真正的模式。
可以用归纳法证明(原文附录 A.9)每步Grow-Improve的完成是单调的,最终最小化经验分布和后验分布的KL。
ReST\^{EM}
\(ReST^{EM}\) (2024/04)是基于EM算法对ReST做的扩展,针对有标量反馈的场景(数学等),并scale到各种尺寸的LLM上。

- 数学解释充分:基于EM的收敛性证明
- 无需混合原始数据,每个E步构造生成数据,但每个M步从基座开始优化,不继承前一步的模型
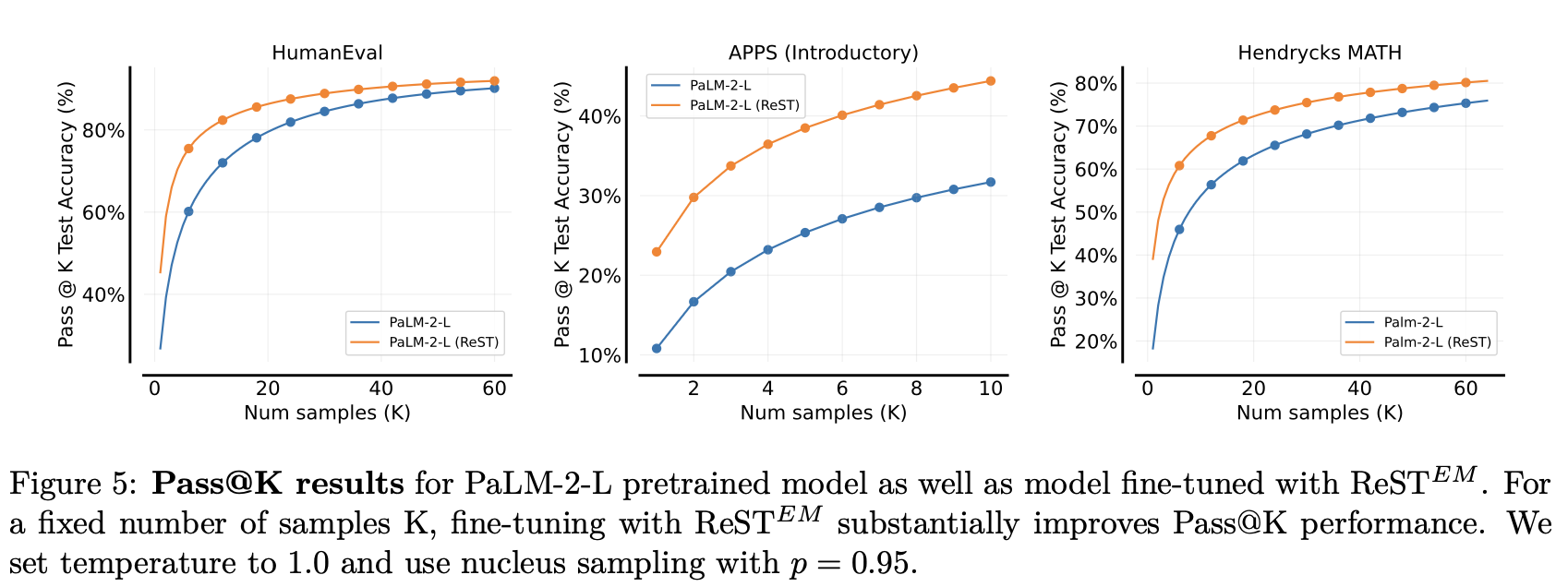
结论1: 可应用到不同规模的模型(Palm2 S & L)
结论2: 比用人类标签更好
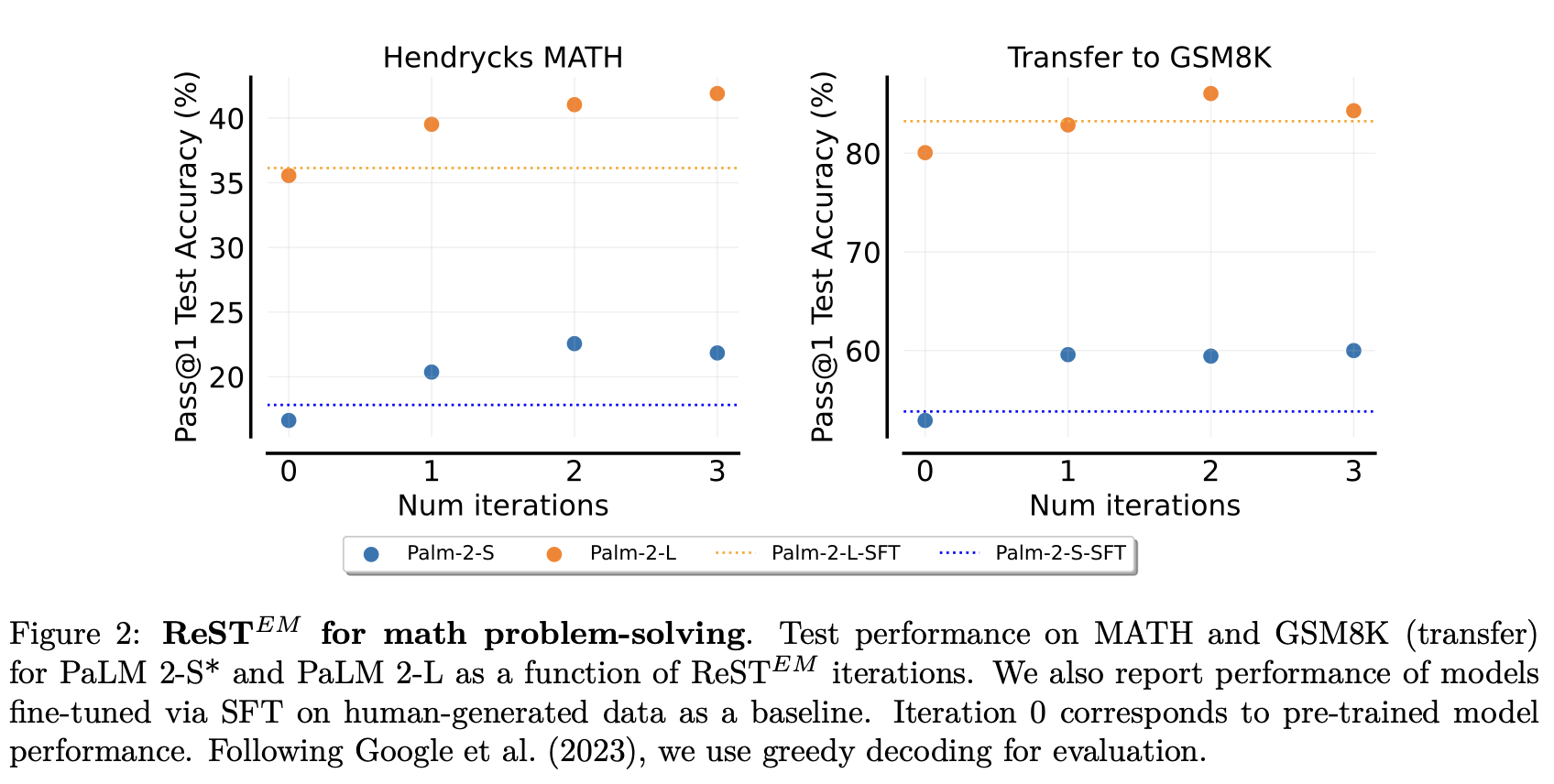
结论3: 存在小数据的过拟合
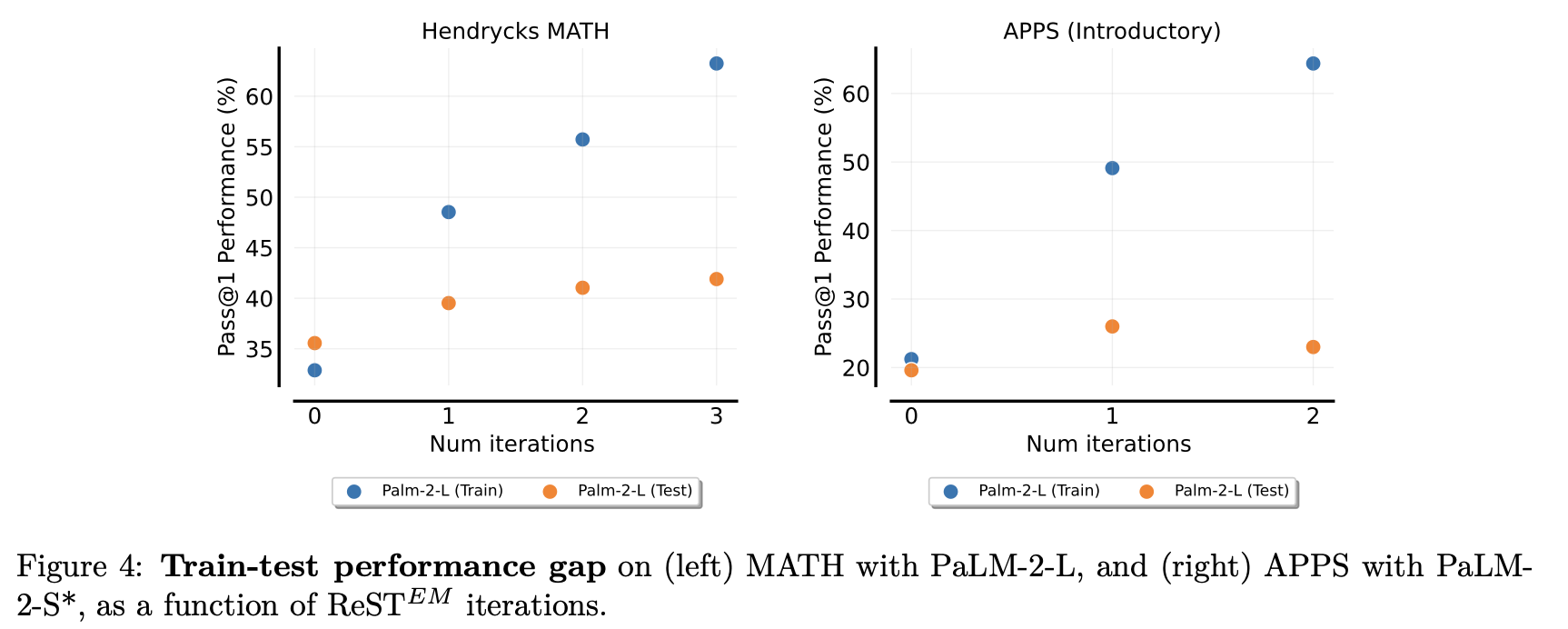
结论4: 提升sampling效率
Re-ReST
Reflection-Reinforced Self-Training,主要提出训练一个大模型反思怪,代替ReST中基于采样的样本生成方法:
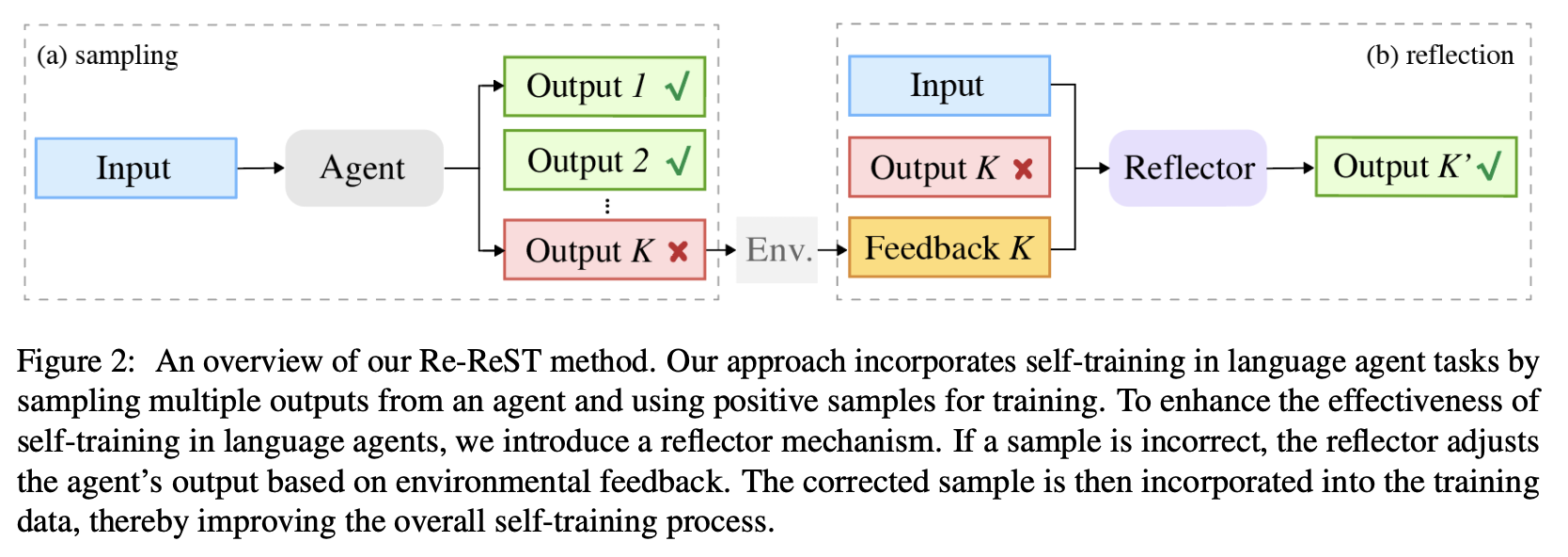
- 相比直接采样,反思怪模型能获得更高效的样本
- 增加自训练的数据量也不一定比只用反思样本强
- 运行时可以使用自一致性代替反思(开销太大,我们不考虑)
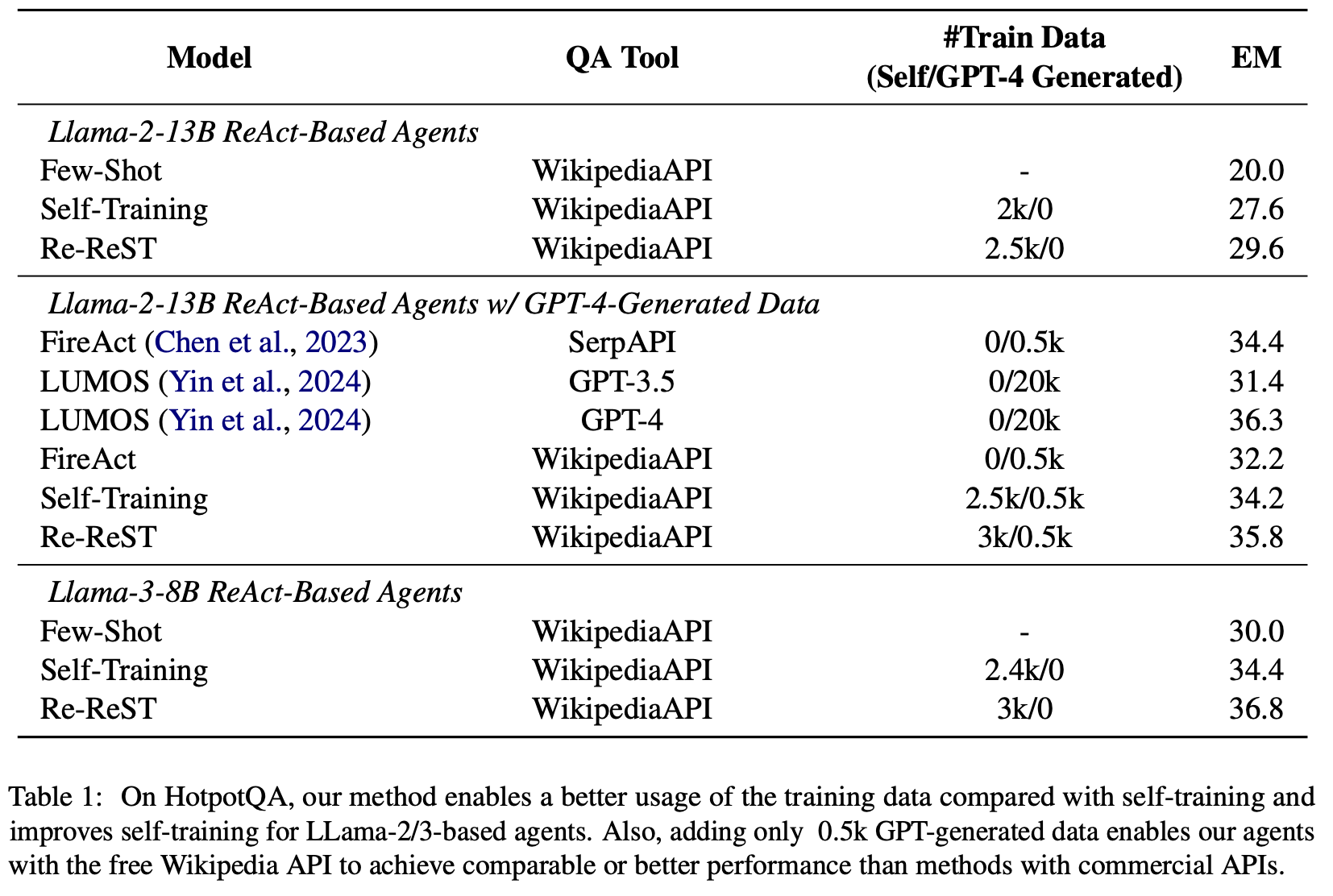
更高效的采样
- ReST-MCTS: 加入过程奖励(PRM),使用MCTS找到更好的样本,同时更新PRM
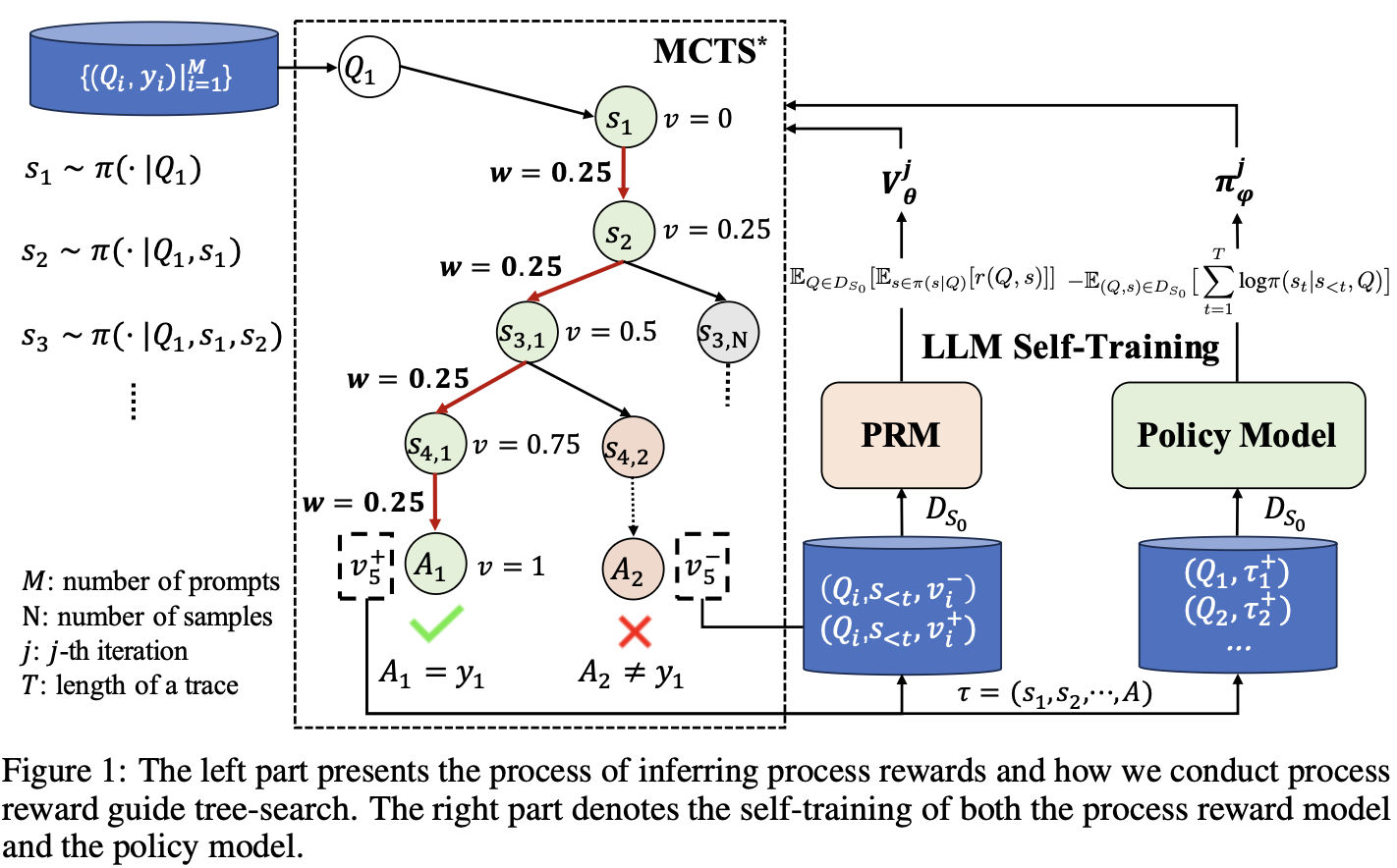
- Entropy-Based Adaptive Weighting for Self-Training: http://arxiv.org/abs/2503.23913
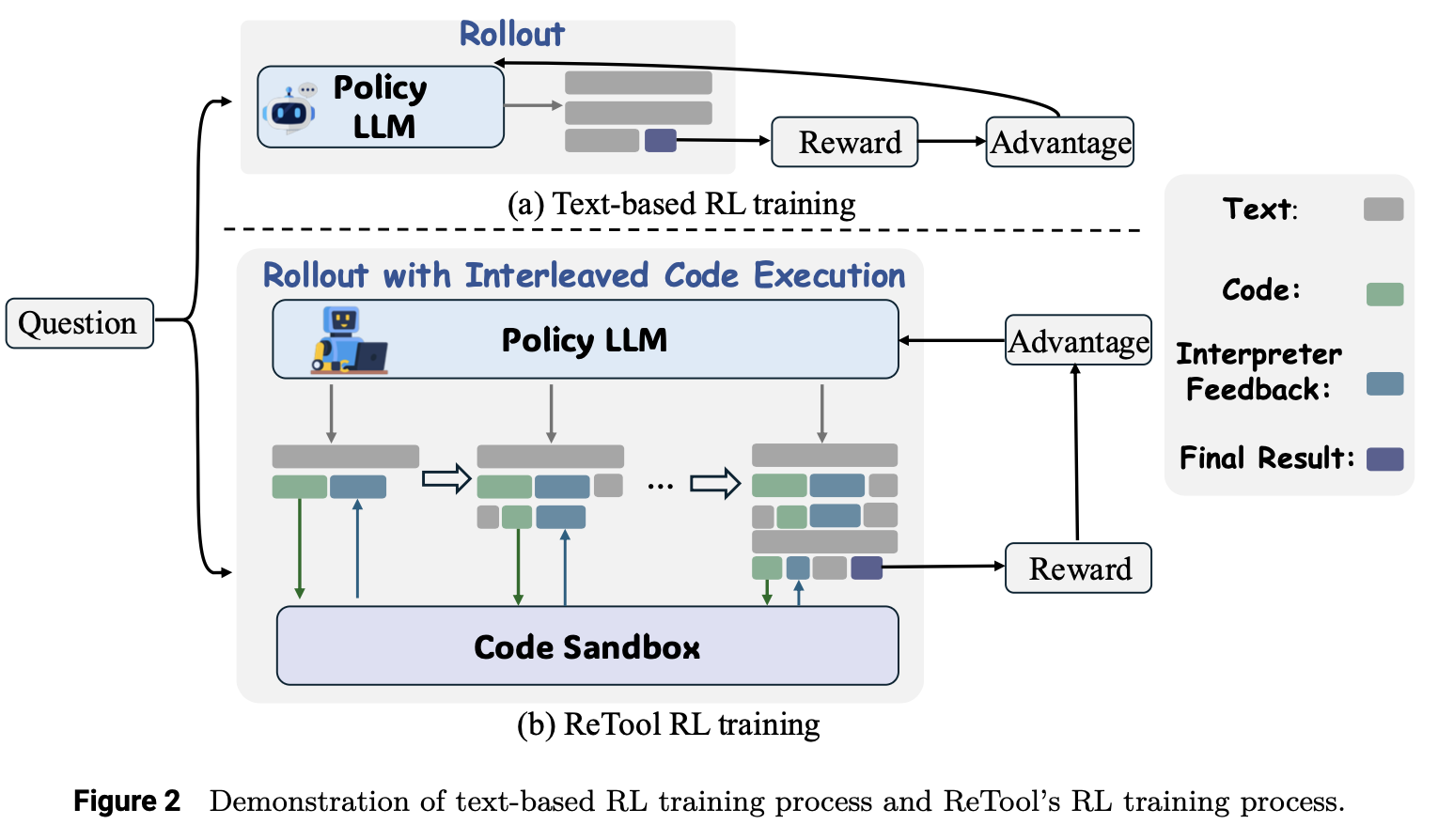
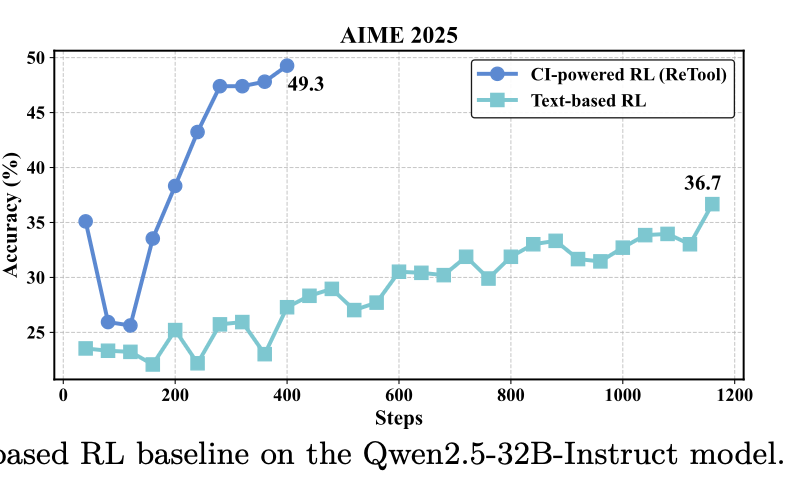
- ReTool: Reinforcement Learning for Strategic Tool Use in LLMs: http://arxiv.org/abs/2504.11536
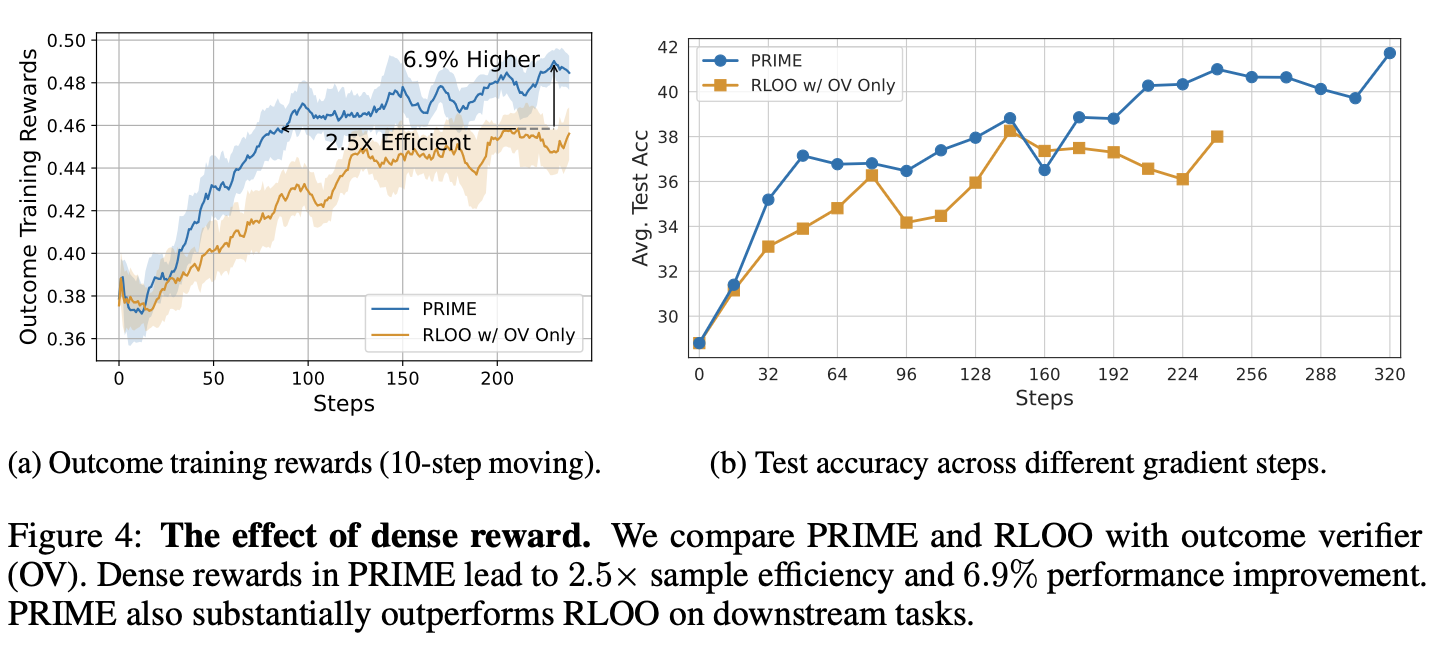
5. PRIME
Process Reinforcement through Implicit Rewards:用ORM训练的模型可以当作一个PRM,以对数似然比作为局部奖励。使用时也会同步更新PRM。可以结合不同的强化学习算法验证,但不能脱离ORM。
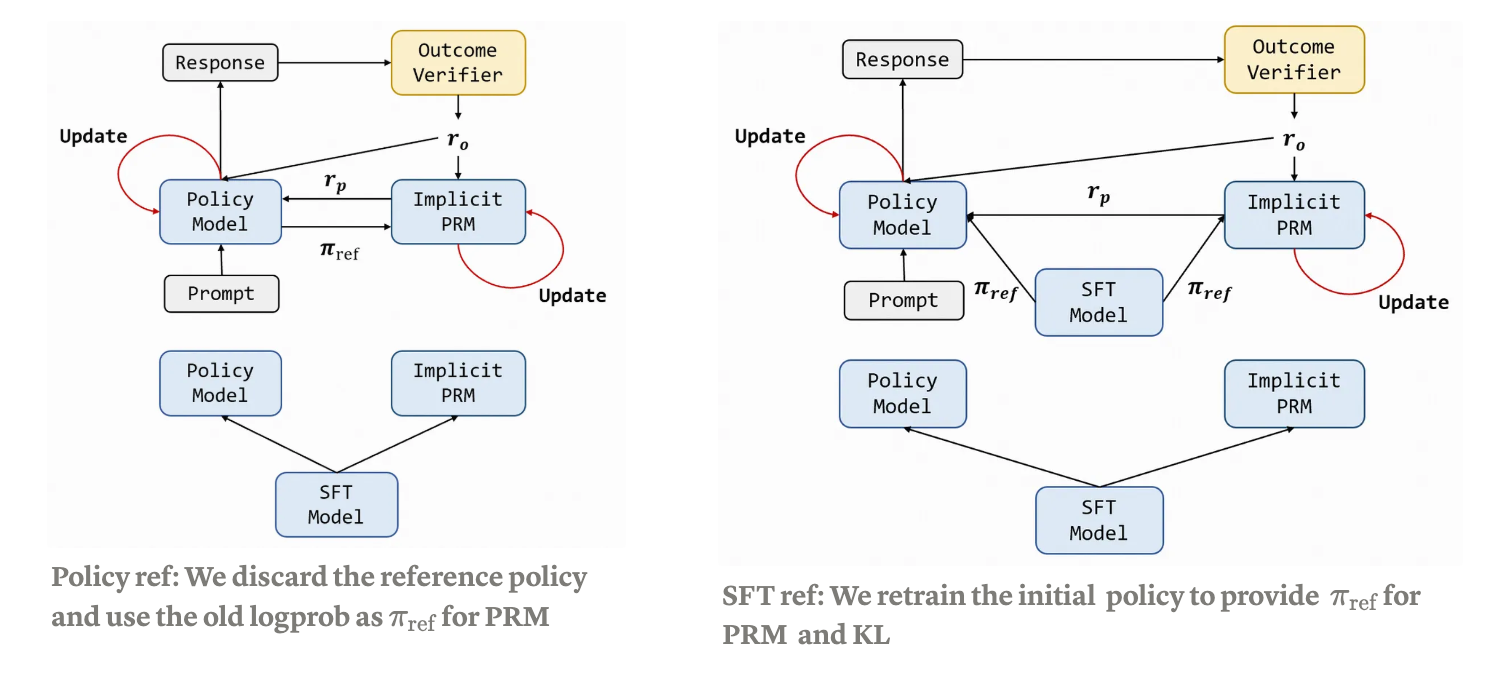

解决三大困难:
- 过程奖励难定义:token-level dense rewards with outcome rewards
- 在线过程更新规模上不去:隐式的过程奖励
- 奖励模型的额外代价:PRM直接从SFT模型得出
6. Generative Verifier
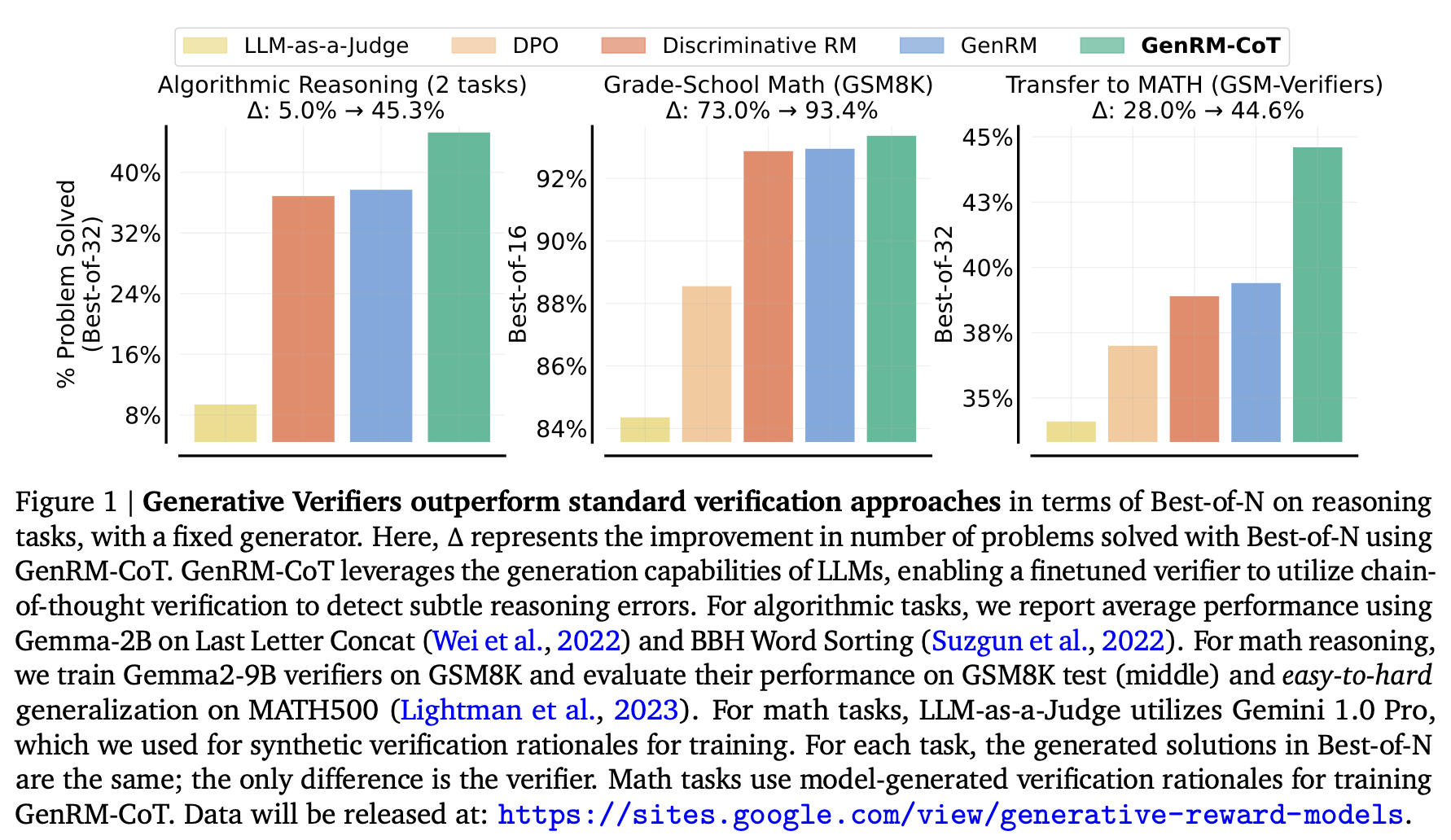
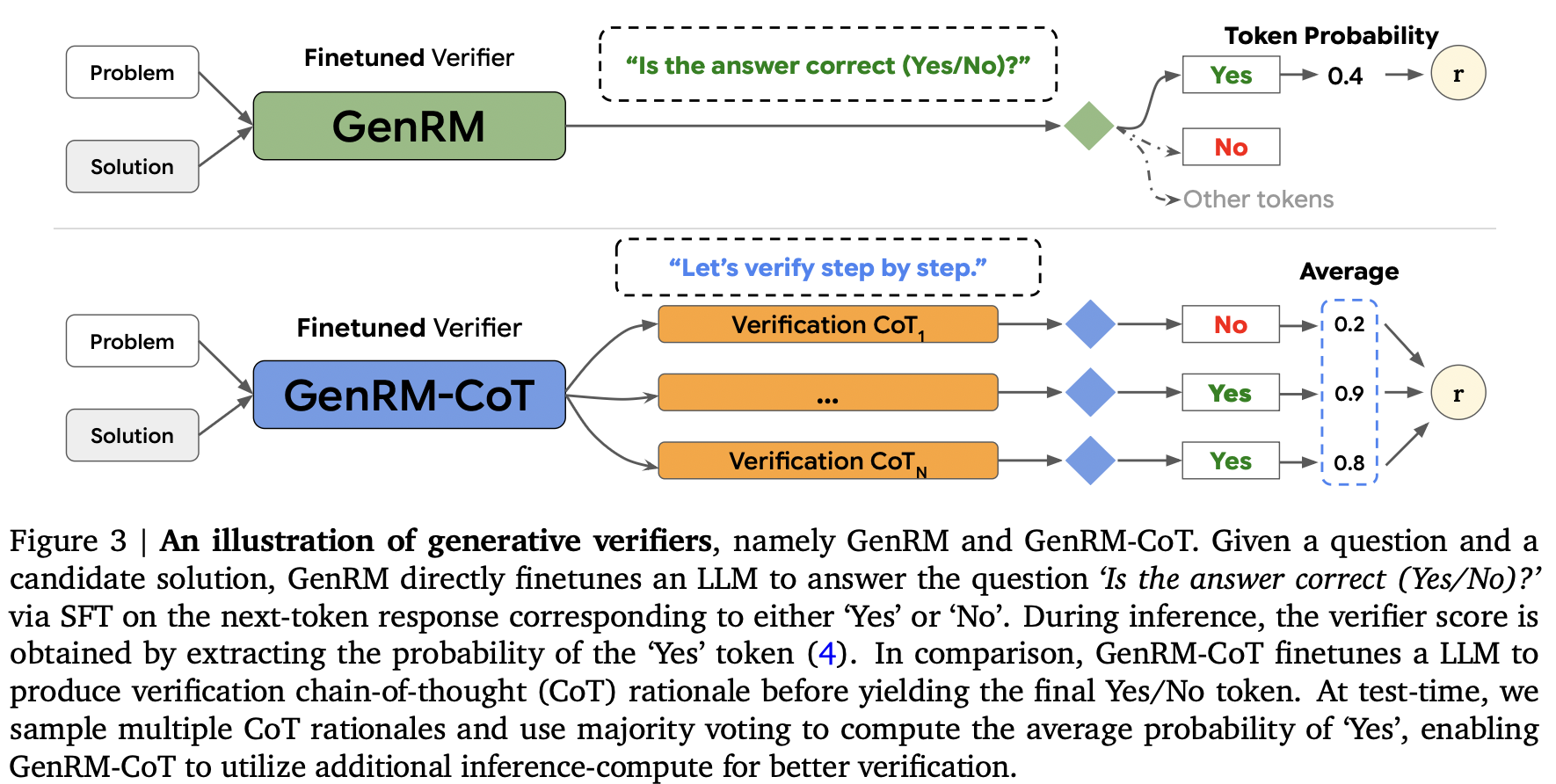
Generative Verifier: 形似GRM,但CoT数据使用形式化合成(代码)或Gemini 1.0 Pro,使用最基础的SFT来训练一个生成式的RM。属于GenRM的一支。
CoT构造:合成(代码)、Gemini 1.0 Pro(数学)

When To Solve, When To Verify: Compute-Optimal Problem Solving and Generative Verification for LLM Reasoning: 强调比较有没有必要用Verifier,主要结论是限定了轨迹数目前提下GenRM能更多更好,但在限定了计算量情况下不需要SC也足够。
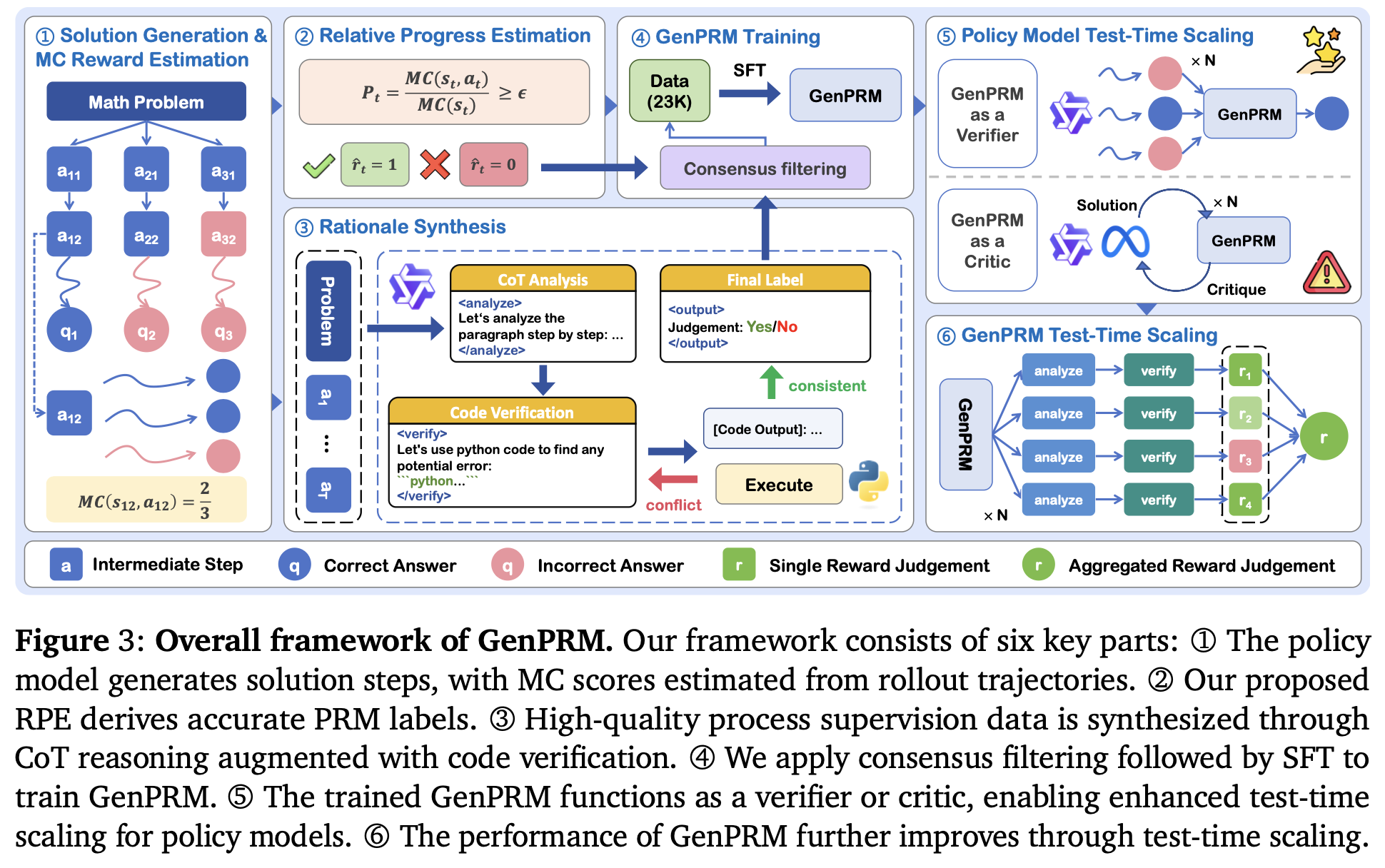
GenPRM: Scaling Test-Time Compute of Process Reward Models via Generative Reasoning
Process Reward指步骤而非token级别,创新性一般。
7. Inference-Scaling
LaTRO
Language Models are Hidden Reasoners: Unlocking Latent Reasoning Capabilities via Self-Rewarding
理据的贝叶斯推断:
\[\begin{aligned} \log \pi_{\theta}({y}|{x}) &= \log \int \pi_{\theta}({y}|{x} \oplus {z}) \pi_0({z}|{x}) d{z} \\ &= \log \int \pi_{\theta}({y}|{x} \oplus {z}) \frac{q({z}|{x})}{q({z}|{x})} \pi_0({z}|{x}) d{z} \\ &\geq \max_{q({z}|{x})} \mathbb{E}_{q({z}|{x})} \big[ \log \pi_{\theta}({y}|{x} \oplus {z}) \big] - D_{\text{KL}}[q({z}|{x}) \|\pi_0({z}|{x})] \end{aligned}\]更进一步,为了简单训练,直接把当前模型自身作为q函数:
\[\max _{\theta} J(\theta):=\mathbb{E}_{(\mathbf{x}, y) \sim \mathcal{D}_{\text{Gold}}}\!\left[\mathbb{E}_{z \sim \pi_{\theta}(\cdot \mid \mathbf{x})}\!\left[\underbrace{\log \pi_{\theta}(y \mid \mathbf{x} \oplus z)}_{R_{\theta}(z, y, \mathbf{x})}\right]-D_{\text{KL}}[\pi_{\theta}(z \mid \mathbf{x}) \| \pi_0(z \mid \mathbf{x})]\right]\]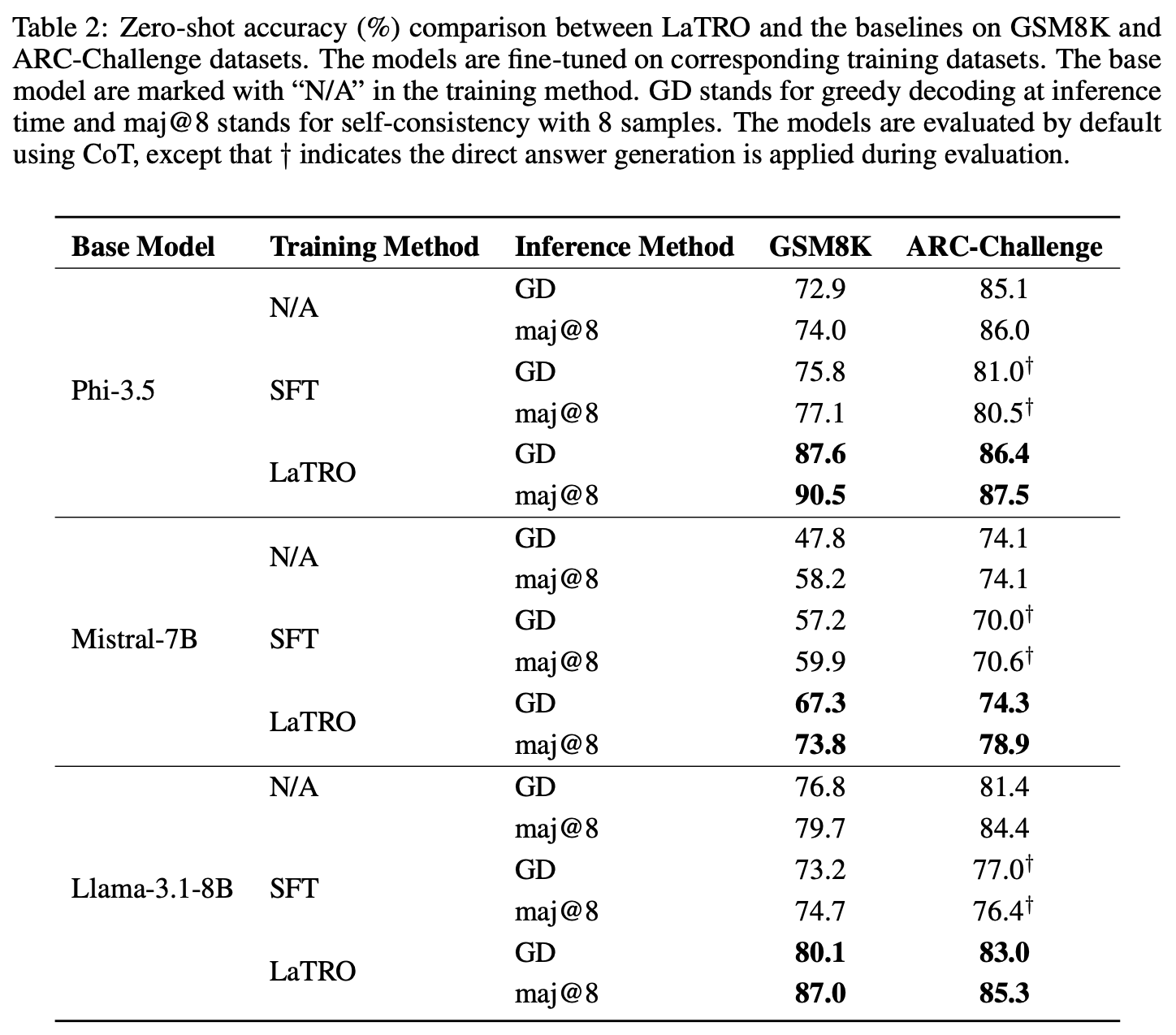
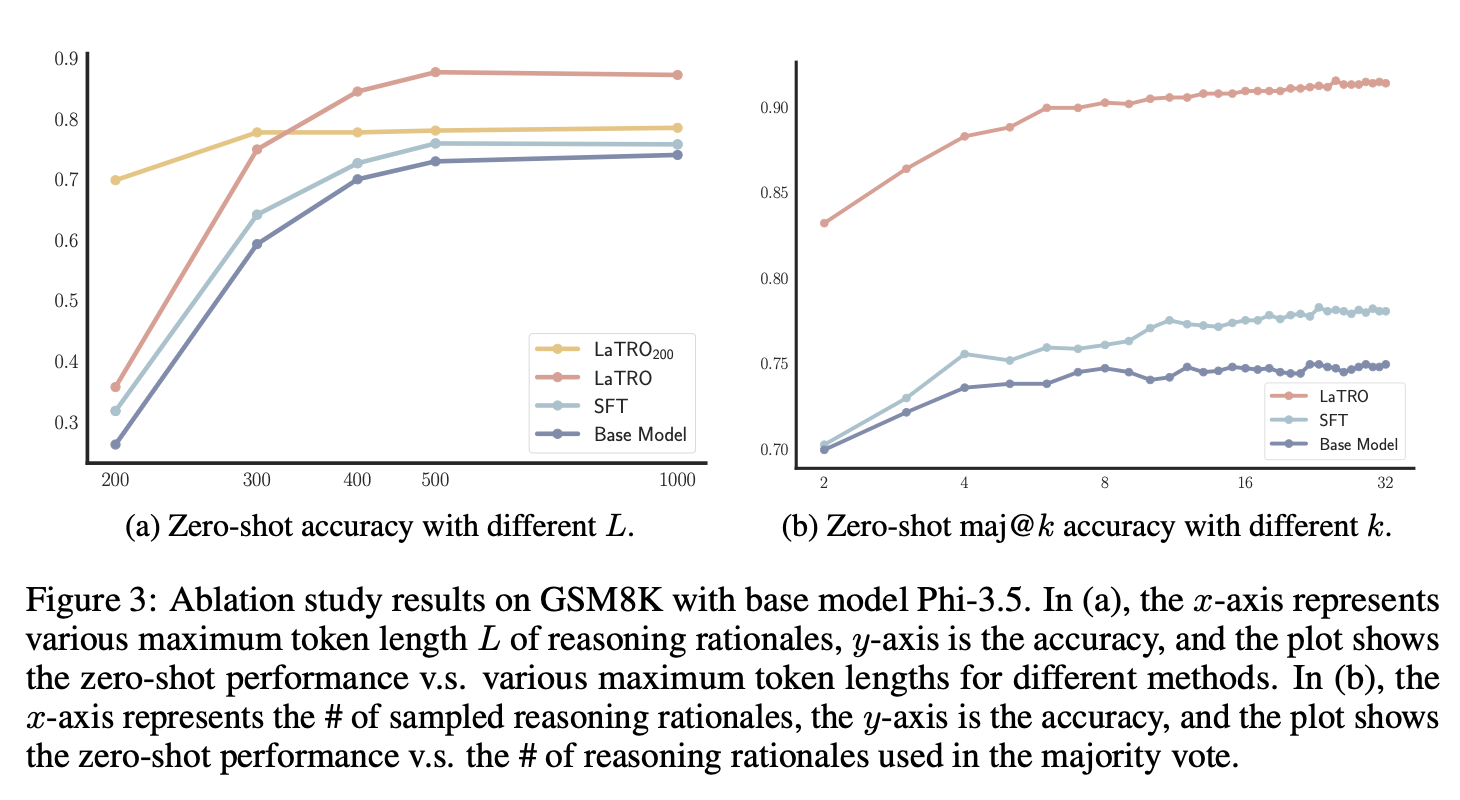
RE
On Reward Functions For Self-Improving Chain-of-Thought Reasoning Without Supervised Datasets (Abridged Version)
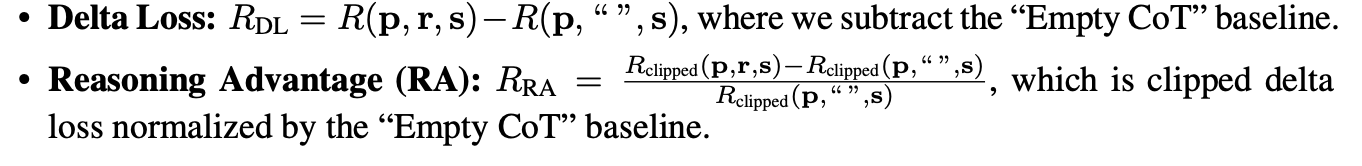

本文使用署名协议进行授权.